Domino and Tromino Tiling in C++

Suppose we have two types of shapes, Domino and Tromino. They can be rotated like below −

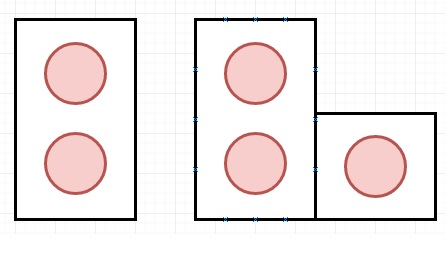
In a tiling, every square must be covered by a tile. Here two tilings are different if and only if there are two 4-directionally adjacent cells on the board such that exactly one of the tilings has both squares occupied by a tile.

Given N, then we have to find in how many ways we can tile 2xN board? So if the input is 3, then the output will be 5. So the arrangements can be [XYZ XXZ XYY XXY XYY] and [XYZ YYZ XZZ XYY XXY], here different letters are used for different tiles.

To solve this, we will follow these steps −

Make an array called dp of size N + 5, set dp[1] := 1, dp[2] := 2 and dp[3] := 5
for i in range 4 to N
- dp[i] := 2*dp[i – 1] + dp[i – 3]
return dp[N]

Example(C++)

Let us see the following implementation to get a better understanding −

Live Demo

#include <bits/stdc++.h>
using namespace std;
const int MOD = 1e9 + 7;
int add(int a, int b){
   return ((a % MOD) + (b % MOD)) % MOD;
}
class Solution {
   public:
   int numTilings(int N) {
      vector <int> dp(N + 5);
      dp[1] = 1;
      dp[2] = 2;
      dp[3] = 5;
      for(int i = 4; i <= N; i++){
         dp[i] = add(2 * dp[i - 1], dp[i - 3]);
      }
      return dp[N];
   }
};
main(){
   Solution ob;
   cout << (ob.numTilings(3));
}

Input

Output

Arnab Chakraborty

Published on 02-May-2020 09:04:13

Previous Page Print Page