Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
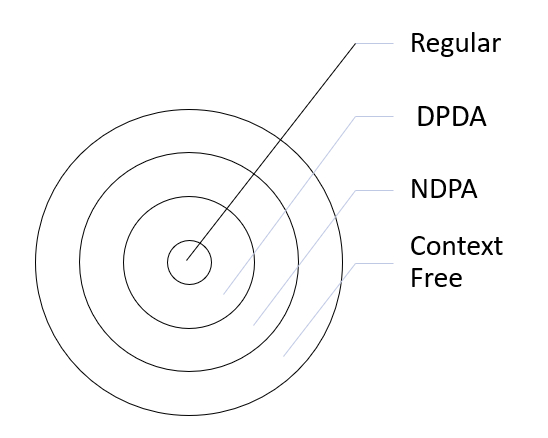
Distinguish between DPDAs and NPDAs in TOC?
Similar to the finite automata (FA), push-down automata (PDA) can be either deterministic or non-deterministic.
A deterministic push down automata (DPDA) never has a choice of the next step −
It has the possible output for every combination of state, input character and stack character, as compared to the deterministic finite automata (DFA).
We need to be careful about every combination of state and stack character. Only one of the transactions is allowed either for the empty symbol ∧ or for an input symbol. Or there can be no transaction at all.
Example
A non-deterministic push-down automaton (NPDA) can contain the following instructions, but a DPDA cannot have these instructions.
Ex1 − (0, a, $,push(Y), 0); (0, a, $,pop, 1)
Ex2 − (0, ∧, $, pop, 3); (0, b, $, nop, 2)
Example
Consider the even length palindromes − L = {wwR | w ∈ {a, b}+}
The transition diagram is as follows −
This was an example of a NPDA, because from state 0, it branches, either loading another letter on or trying to take letters off. This could only be done non-deterministically.
A DPDA would need to know when to start removing letters from the stack. Thus an NPDA can recognise the language of the even palindromes, but a DPDA cannot.
DPDAs recognise the regular languages and also some which are not regular, but not all of the context free languages.
The diagram given below depicts the difference between DPDA and NPDA, when it comes to recognising regular languages and context free grammar −
4K+ Views
