- Trending Categories
Data Structure
Networking
RDBMS
Operating System
Java
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Distance between Vertices and Eccentricity
Distance between Two Vertices
It is number of edges in a shortest path between Vertex U and Vertex V. If there are multiple paths connecting two vertices, then the shortest path is considered as the distance between the two vertices.
Notation − d(U,V)
There can be any number of paths present from one vertex to other. Among those, you need to choose only the shortest one.
Example
Take a look at the following graph −
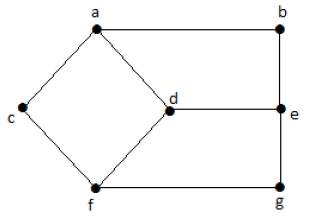
Here, the distance from vertex 'd' to vertex 'e' or simply 'de' is 1 as there is one edge between them. There are many paths from vertex 'd' to vertex 'e' −
- da, ab, be
- df, fg, ge
- de (It is considered for distance between the vertices)
- df, fc, ca, ab, be
- da, ac, cf, fg, ge
Eccentricity of a Vertex
The maximum distance between a vertex to all other vertices is considered as the eccentricity of vertex.
Notation − e(V)
The distance from a particular vertex to all other vertices in the graph is taken and among those distances, the eccentricity is the highest of distances.
Example
In the above graph, the eccentricity of 'a' is 3.
The distance from 'a' to 'b' is 1 ('ab'),
from 'a' to 'c' is 1 ('ac'),
from 'a' to 'd' is 1 ('ad'),
from 'a' to 'e' is 2 ('ab'-'be') or ('ad'-'de'),
from 'a' to 'f' is 2 ('ac'-'cf') or ('ad'-'df'),
from 'a' to 'g' is 3 ('ac'-'cf'-'fg') or ('ad'-'df'-'fg').
So the eccentricity is 3, which is a maximum from vertex 'a' from the distance between 'ag' which is maximum.
In other words,
e(b) = 3
e(c) = 3
e(d) = 2
e(e) = 3
e(f) = 3
e(g) = 3
Radius of a Connected Graph
The minimum eccentricity from all the vertices is considered as the radius of the Graph G. The minimum among all the maximum distances between a vertex to all other vertices is considered as the radius of the Graph G.
Notation − r(G)
From all the eccentricities of the vertices in a graph, the radius of the connected graph is the minimum of all those eccentricities.
Example − In the above graph r(G) = 2, which is the minimum eccentricity for 'd'.
Diameter of a Graph
The maximum eccentricity from all the vertices is considered as the diameter of the Graph G. The maximum among all the distances between a vertex to all other vertices is considered as the diameter of the Graph G.
Notation − d(G)
From all the eccentricities of the vertices in a graph, the diameter of the connected graph is the maximum of all those eccentricities.
Example − In the above graph, d(G) = 3; which is the maximum eccentricity.
- Related Questions & Answers
- How can we measure the similarity or distance between two vertices in a graph?
- Edges and Vertices of Graph
- Calculate distance and duration between two places using google distance matrix API in Python?
- Count all possible paths between two vertices in C++
- Find maximum distance between any city and station in C++
- Find maximum distance between any city and station in Python
- Shortest distance between objects in JavaScript
- Increase the distance between the title and the plot in Matplotlib
- Smallest Distance Between Two Words in Python
- Longest distance between 1s in binary JavaScript
- JavaScript - find distance between items on array
- Hamming Distance between two strings in JavaScript
- Connectivity, Distance, and Spanning Trees
- Program to find maximum distance between empty and occupied seats in Python
- Maximum and minimum isolated vertices in a graph in C++