Difference between Backtracking and Branch-N-Bound technique

The Backtracking technique is an algorithm used to solve the decision problem whereas the Branch-N-Bound technique is an algorithm used to solve the optimization problem. Both techniques follow the brute force method and are used to generate the State Space tree. A State Space tree is the tree that represents the nodes in all possible states of the problem from a root node to the terminal node.

Let us learn both techniques one by one and understand the difference in detail.

Backtracking Technique

Backtracking is the modified process of the brute force approach where the technique efficiently searches for a solution to the problem among all available options.

The brute force approach is nothing but it finds all possible solutions to make satisfaction to the given problem.

Example of Brute force approach −

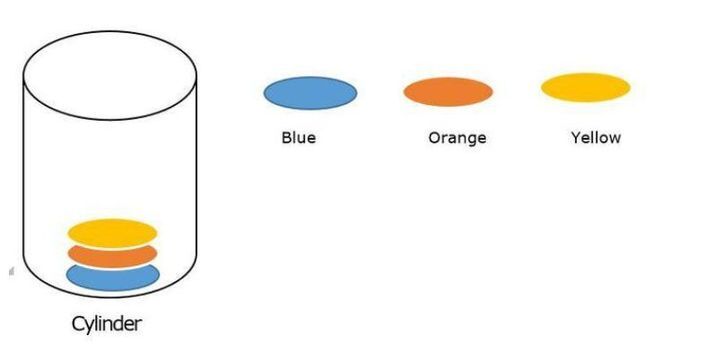
In the given figure there are three colors to fill into the cylinder by all possible solutions using the brute force approach.

The following ways to fill the color into the cylinder are −

• Blue, Orange, Yellow

• Blue, Yellow, Orange

• Orange, Blue, Yellow

• Orange, Yellow, Blue

• Yellow, Blue, Orange

• Yellow, Orange, Blue

There are a total of 6 ways to fill the color into the cylinder and that is the way we can modify the solution in the backtracking.

The following important point related to backtracking −

• A backtracking solution can be represented in the form of a tree and it is also called a State Space tree.

• Backtracking follow the Depth-first search(DFS).

In this given figure we made a tree solution approach using backtracking.

• Depending upon the constraints we solve the solution based on the constraints. For example, we remove the orange from the end of every node and this shows the reduction of time complexity of the problem.

• It involves a feasibility problem.

Branch-N-Bound Technique

The branch-N-bound technique is an algorithm used to solve the problem of optimization by breaking it down into smaller subproblems and by bounding function it eliminates the subproblem that doesn’t contain an optimal solution.

Branch and bound search is a way to combine space saving of depth-first search with heuristics information. The idea of branch and bound search is to maintain the lowest cost path or minimal path.

This technique contains two parts −

• Branch − Several choices are found

• Bound − Setting bound on solution quality.

The Branch-N-Bound follows the Breath First Search.

Now we are finding the route of R to G using BFS and creating the tree.

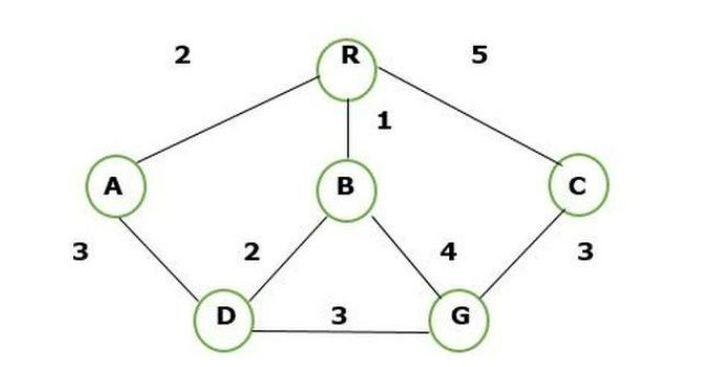
The following step to solve the BFS approach is given below −

Step 1 − We know the source or root node is R.

Step 2 − Visit the successor node of a root node i.e, A, B, and C.

Step 3 − Expand the path node of A to D, B to D and B to G, and C to G.

Step 4 − Now the complete structure becomes

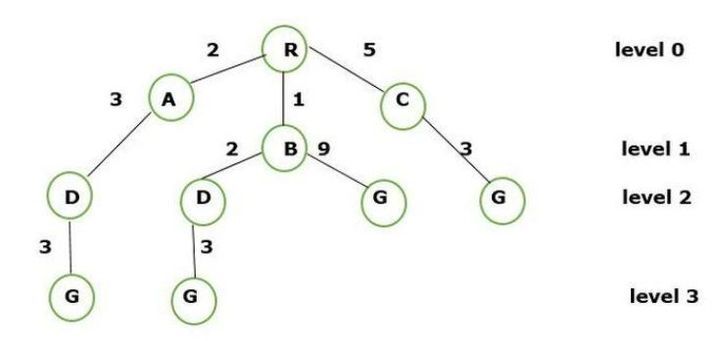
The leveling space partition of tree structure nodes are −

Level 0 − R

Level 1 − R -> A, R-> B, R -> C

Level 2 − R -> A -> D, R -> B -> D and R -> B -> G, R -> C -> G

Level 3 − Finally, the connecting path and calculation of node weight look like

R -> A -> D -> G( 3+3+2 = 8 ), R -> B -> D -> G ( 3+2+1 = 6 ) and R -> B -> G ( 9+1 = 10), R -> C -> G( 5+3 = 8 )

We have the shortest route from node R – G is

R -> B -> D -> G = (3+2+1) = 6

So this way we solve the approach of breath first search.

The following important point related to Branch-N-Bound −

• This technique traverses in any manner DFS or BFS.

• It involves a binding function.

• It completely searches the state space tree by targeting the optimal solution.

Difference between Backtracking VS Branch-N-Bound technique

Parameters	Backtracking	Branch-N-Bound
Why it is used?	This is used to solve the decision-based problem.	This is used to solve the optimization problem.
Nodes	This is a state space tree where the node explored the depth-first search.	This explored the optimization problem.
Efficient	More efficient.	Less Efficient.
Function	It involves the feasibility function.	It involves the bounding function.
Traverse	It traverses the tree by depth-first search	It traverses the tree by breadth-first search
Solves	Backtracking can solve the game of chess and sudoku.	It doesn’t solve any game problem.
Application Used	This application is used to solve the N-queen problem, the Hamilton cycle, and the problem based on graph coloring.	This type of application is used to solve the problem based on the Travelling salesman problem.

Conclusion

We saw the differences between two algorithms and the better approach is Branch-N_Bound which follows the BFS search. Secondly, the best part of Branch-N-Bound is that it is targeted at an optimal solution whereas in backtracking the targeted node are based on a decision problem. While solving these problem statements the BFS requires more memory as compared to DFS.