
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to print the diamond shape
In this article, we will learn how to print a diamond shape with 2n rows and n columns for a given size n using C++.
For example, if n = 4, the diamond shape will look like this:
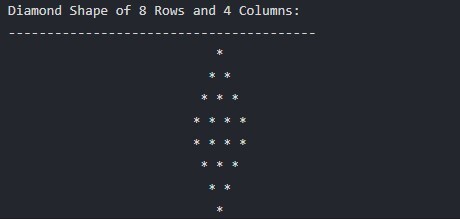
Algorithm to Print Diamond Shape
To print the diamond shape, we can follow these steps:
- Take an integer input n from the user.
- To print upper half of the diamond, use a loop that runs from i = 1 to i <= n.
- In each iteration of the loop, print empty spaces from j = 1 to j = n - i
- Then, print stars from j = 1 to j <= i.
- After printing the stars of each row, print a newline character to move to the next line.
- Now, to print the lower half of the diamond, use a loop that runs from i = n to i >= 1.
- Use the same code as above to print empty spaces and stars for the lower half.
C++ Program to Print Diamond Shape
The C++ code below, implements the above algorithm to print a diamond shape. This consist of two separate nested loops for the upper and lower halves of the diamond.
#include <iostream>
using namespace std;
int main() {
int n = 6; // Height of the upper half
cout << "Diamond Shape of " << 2*n << " Rows and " << n << " Columns:" << endl;
cout << "----------------------------------------" << endl;
// Upper half of the diamond
for (int i = 1; i <= n; ++i) {
// Print spaces
for (int j = 1; j <= n - i; ++j)
cout << " ";
// Print stars
for (int j = 1; j <= i; ++j)
cout << "* ";
cout << endl;
}
// Lower half of the diamond
for (int i = n; i >= 1; --i) {
// Print spaces
for (int j = 1; j <= n - i; ++j)
cout << " ";
// Print stars
for (int j = 1; j <= i; ++j)
cout << "* ";
cout << endl;
}
return 0;
}
The output of the above code will be:
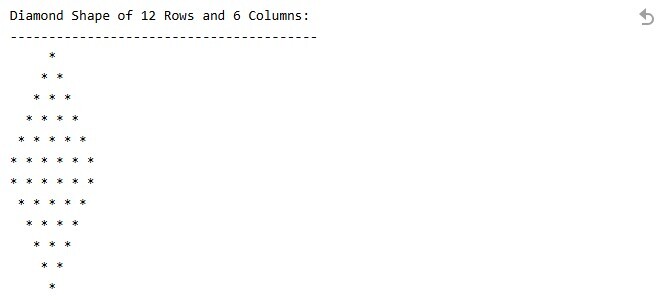
Time and Space Complexity
Time Complexity: The time complexity of this algorithm is O(n^2), where n is the number of rows in the upper half of the diamond.
Space Complexity: The space complexity is O(1) since we are not storing any data in program.

Advertisements
