Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to find out the number of cells to block in a grid to create a path
Suppose, there is a grid of dimensions h * w. There is a robot in cell position (0, 0) and it has to go to the position (h - 1, w - 1). There are two types of cells in a grid, blocked and unblocked. The robot can pass through the unblocked cells but cannot pass through the blocked cells. The robot can go in four directions; it can go left, right, up, and down. But the robot may go in any direction from a cell to another (ignoring the previous cell it was in), so we have to make only one path and block all the other cells that are not in that path. We have to find out and return how many cells we have to block to make one path for the robot from (0, 0) to (h - 1, w - 1) and if there is no path possible, we return -1.
So, if the input is like h = 4, w = 4, grid = {"..#.", "#.#.", "#.##", "#..."}, then the output will be 2.
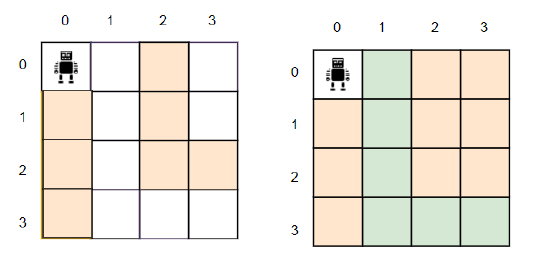
We have to block only two cells to create a single path from (0, 0) to (3, 3).
To solve this, we will follow these steps −
Define one 2D array dp
dp[0, 0] := 0
Define an array moves containing pairs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}}
Define one queue q
insert pair (0, 0) at the end of q
while (not q is empty), do:
p := first element of q
delete first element from q
for initialize i := 0, when i < 4, update (increase i by 1), do:
row := first value of p + first value of moves[i]
col := second value of p + second value of moves[i]
if row < 0 or row > h - 1 or col < 0 or col > w - 1, then:
Ignore following part, skip to the next iteration
if grid[row, col] is same as '#', then:
Ignore following part, skip to the next iteration
if dp[first value of p, second value of p] + 1 < dp[row, col], then:
dp[row, col] := dp[first value of p, second value of p] + 1
insert pair(row, col) into q
if dp[h - 1, w - 1] is same as 2500, then:
return -1
count := 0
for initialize i := 0, when i < h, update (increase i by 1), do:
for initialize j := 0, when j < w, update (increase j by 1), do:
if grid[i, j] is same as '.', then:
(increase count by 1)
return count - (dp[h - 1, w - 1] + 1)Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
int solve(int h, int w, vector<string> grid){
vector<vector<int>> dp(h, vector<int>(w, 2500));
dp[0][0] = 0;
vector<pair<int, int>> moves = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
queue<pair<int, int>> q;
q.push(make_pair(0, 0));
while (!q.empty()) {
auto p = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int row = p.first + moves[i].first;
int col = p.second + moves[i].second;
if (row < 0 || row > h - 1 || col < 0 || col > w - 1) continue;
if (grid[row][col] == '#')
continue;
if (dp[p.first][p.second] + 1 < dp[row][col]) {
dp[row][col] = dp[p.first][p.second] + 1; q.push(make_pair(row, col));
}
}
}
if (dp[h - 1][w - 1] == 2500) {
return -1;
}
int count = 0;
for (int i = 0; i < h; i++) {
for (int j = 0; j < w; j++) {
if (grid[i][j] == '.') count++;
}
}
return count - (dp[h - 1][w - 1] + 1);
}
int main() {
int h = 4, w = 4;
vector<string> grid = {"..#.", "#.#.", "#.##", "#..."};
cout<< solve(h, w, grid);
return 0;
}Input
4, 4, {"..#.", "#.#.", "#.##", "#..."}
Output
2
289 Views
