C++ program to count expected number of operations needed for all node removal

Suppose we have the adjacency matrix of a directed graph G. Until the graph becomes empty, we are repeating the following operation: Select one vertex from G, then erase that vertex and all vertices that are reachable from that vertex by following some edges. Erasing a vertex will also erase the edges incident to it. We have to find the expected number of times the operation is done

So, if the input is like

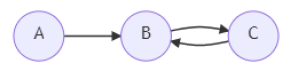
then the output will be 1.6667, because initially select vertex A, remove all vertices, if we select vertex B, remove B and C, and in second operation select A to remove it, similarly by selecting C also it takes 2 operations. So the average is (1+2+2)/3 = 1.6667.

Steps

To solve this, we will follow these steps −

n := size of G
for initialize i := 0, when i < n, update (increase i by 1), do:
   G[i, i] := 1
for initialize k := 0, when k < n, update (increase k by 1), do:
   for initialize i := 0, when i < n, update (increase i by 1), do:
      for initialize j := 0, when j < n, update (increase j by 1), do:
         if G[i, k] is non-zero and G[k, j] is non-zero, then:
            G[i, j] := 1
         ans := 0
      for initialize i := 0, when i < n, update (increase i by 1), do:
         k := 0
      for initialize j := 0, when j < n, update (increase j by 1), do:
         if G[j, i] is non-zero, then:
            (increase k by 1)
         ans := ans + 1.0 / k
return ans

Example

Let us see the following implementation to get better understanding −

#include <bits/stdc++.h>
using namespace std;

double solve(vector<vector<int>> G){
   int n = G.size();
   for (int i = 0; i < n; ++i)
      G[i][i] = 1;
   for (int k = 0; k < n; ++k)
      for (int i = 0; i < n; ++i)
         for (int j = 0; j < n; ++j)
            if (G[i][k] && G[k][j])
               G[i][j] = 1;
   double ans = 0;
   for (int i = 0; i < n; ++i){
      int k = 0;
      for (int j = 0; j < n; ++j)
         if (G[j][i])
            ++k;
         ans += 1.0 / k;
   }
   return ans;
}
int main(){
   vector<vector<int>> G = { { 0, 1, 0 }, { 0, 0, 1 }, { 0, 1, 0 }};
   cout << solve(G) << endl;
}

Input

{ { 0, 1, 0 }, { 0, 0, 1 }, { 0, 1, 0 } }

Output

1.66667