
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Compute Discrete Fourier Transform Using Naive Approach
DFT stands for Discrete Fourier Transform. DFT is a mathematical technique in which we convert the signals of the time domain to their respective signal in the frequency domain, i.e., converting into a list of numbers that tell us which frequencies are present in that signal. Here, by time signal, we mean signals such as audio, temperature, etc that changes over time. The frequency signal means the frequency of each signal present in the time signal.
The numbers that tell us which frequencies are present in the signal are called the coefficients. In this article, our task is to compute Discrete Fourier Transform(DFT) using naive approach.
Formula of DFT
The formula to calculate the DFT is mentioned below:
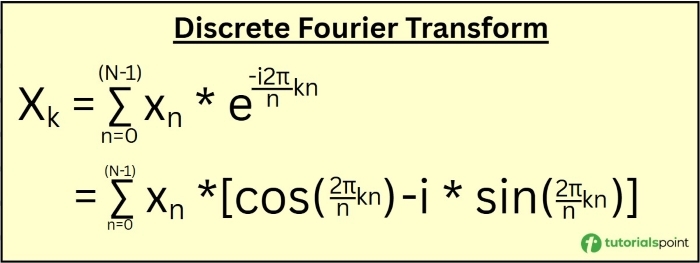
Here, Xn is the signal at index n, N is the total number of signals, and Xk is the coefficient at index k. We have used Euler's formula to expand the first formula into the second formula.
Steps to Compute DFT in C++
The steps to compute the DFT coefficients are as follows:
- First, we choose a linear function. In this case, we have used ai + bi - c. The values of a, b, and c are already given along with the value of k and n.
- We are using Euler's theorem, i.e., e-(i?) = cos(?) - i sin(?), to expand the formula to calculate the DFT. The formula of DFT is mentioned in the above section.
- Then, we have calculated the real and imaginary coefficients using the DFT formula, which is stored in dft_value[j].real and dft_value[j].img, respectively.
- The real and imaginary part of the coefficient together gives the magnitude and phase of the frequency.
- Then, using a for loop, we have printed all the real and imaginary coefficients.
C++ Implementation for Computing DFT
The following program implements the above steps to compute Discrete Fourier Transform(DFT) using naive approach.
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
#define PI 3.14159265
class DFT_Coeff {
public:
double real, img;
DFT_Coeff() {
real = 0.0;
img = 0.0;
}
};
int main() {
const int M = 10; // Number of samples
const int k = 10;
double a = 4.0;
double b = 5.0;
double c = 6.0;
// Calculating function ai + bi - c
double function[M];
for (int i = 0; i < M; i++) {
function[i] = ((a + b) * i - c);
}
vector<DFT_Coeff> dft_value(k);
// Calculating real and imaginary parts of DFT
for (int j = 0; j < k; j++) {
for (int i = 0; i < M; i++) {
double angle = (2.0 * PI * j * i) / M;
dft_value[j].real += function[i] * cos(angle);
dft_value[j].img -= function[i] * sin(angle);
}
}
cout << "DFT Coefficients:\n";
for (int j = 0; j < k; j++) {
cout << "X[" << j << "] = " << dft_value[j].real
<< " - (" << dft_value[j].img << "i)\n";
}
return 0;
}
The output of the above code is as follows:
DFT Coefficients: X[0] = 345 - (0i) X[1] = -45 - (138.496i) X[2] = -45 - (61.9372i) X[3] = -45 - (32.6944i) X[4] = -45 - (14.6214i) X[5] = -45 - (-1.34617e-06i) X[6] = -45 - (-14.6214i) X[7] = -45 - (-32.6944i) X[8] = -45 - (-61.9372i) X[9] = -45 - (-138.496i)

