
 Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program to Compute DFT Coefficients Directly
DFT stands for Discrete Fourier Transform. DFT is a mathematical technique in which we convert the signals of the time domain to their respective signal in the frequency domain, i.e., converting into a list of numbers that tell us which frequencies are present in that signal. Here, by time signal, we mean signals such as audio, temperature, etc. that changes over time. The frequency signal means the frequency of each signal present in the time signal.
The numbers that tell us which frequencies are present in the signal are called the coefficients. In this article, our task is to compute the DFT coefficients.
Formula of DFT
The formula to calculate the DFT is mentioned below:
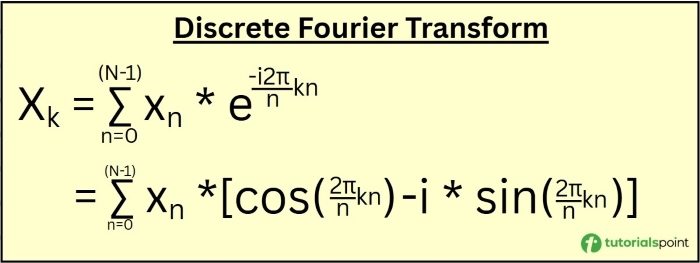
Here, Xn is the signal at index n, N is the total number of signals, and Xk is the coefficient at index k. We have used Euler's formula to expand the first formula into the second formula.
Steps to Compute DFT Coefficients in C++
The steps to compute the DFT coefficients are as follows:
- First, we choose a linear function. In this case, we have used ai + bi - c. The values of a, b, and c are already given along with the value of k and n.
- We are using Euler's theorem, i.e., e-(i?) = cos(?) - i sin(?), to expand the DFT formula that is mentioned in the above image.
- Then, we calculated and printed the real and imaginary coefficients using the DFT formula.
C++ Implementation for Computing DFT Coefficients
The following program implements the above steps to compute the DFT coefficients using the DFT formula.
#include <iostream>
#include <cmath>
using namespace std;
#define PI 3.14159265
class DFT_Coeff {
public:
double real, img;
DFT_Coeff() : real(0.0), img(0.0) {}
};
int main() {
const int N = 10;
const double a = 4.0;
const double b = 6.0;
const double c = 7.0;
const int k = 4;
double function[N];
for (int i = 0; i < N; i++) {
function[i] = (a + b) * i - c;
}
DFT_Coeff dft_value;
for (int i = 0; i < N; i++) {
double angle = (2 * PI * k * i) / N;
dft_value.real += function[i] * cos(angle);
dft_value.img -= function[i] * sin(angle);
}
cout << "DFT Coefficient X[" << k << "] = ";
cout << "(" << dft_value.real << ") - (" << dft_value.img << " i)" << endl;
return 0;
}
The output of the above code is as follows:
DFT Coefficient X[4] = (-50) - (16.246 i)

