Article Categories
- All Categories
-
 Data Structure
Data Structure
-
 Networking
Networking
-
 RDBMS
RDBMS
-
 Operating System
Operating System
-
 Java
Java
-
 MS Excel
MS Excel
-
 iOS
iOS
-
 HTML
HTML
-
 CSS
CSS
-
 Android
Android
-
 Python
Python
-
 C Programming
C Programming
-
 C++
C++
-
 C#
C#
-
 MongoDB
MongoDB
-
 MySQL
MySQL
-
 Javascript
Javascript
-
 PHP
PHP
Selected Reading
Program for Volume and Surface Area of Cube in C++
What is cube?
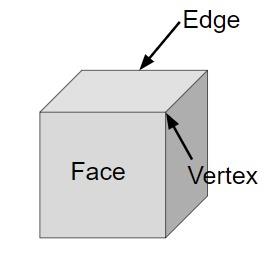
Cube is a three-dimensional object with six faces of square shape which means it has sides of same length and breadth. Cube is the only regular hexahedron with following properties −
- six faces
- 12 edges
- 8 vertices
Given below is the figure of cube
Problem
Given with the side, the task is to find the total surface area and volume of a cube where surface area is the space occupied by the faces and volume is the space that a shape can contain.
To calculate surface area and volume of a cube there is a formula −
Surface Area = 6*Side*side
Volume = Side*side*side
Example
Input-: side=3 Output-: volume of cube is: 27 Total surface area of cube is 54
Algorithm
Start Step 1 -> declare function to find volume of cube double volume(double a) return (a*a*a) Step 2 -> declare function to find area of cube double volume(double a) return (6*a*a) Step 3 -> In main() Declare variable double a=3 Print volume(a) Print area(a) Stop
CODE
#include <bits/stdc++.h>
using namespace std;
// function for volume of cube
double volume(double a){
return (a * a * a);
}
//function for surface area of cube
double area(double a){
return (6 * a * a);
}
int main(){
double a = 3;
cout<< "volume of cube is: "<<volume(a)<<endl;
cout<< "Total surface area of cube is "<<area(a);
return 0;
}
Output
volume of cube is: 27 Total surface area of cube is 54

Advertisements

