Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program for Shortest Job First (SJF) scheduling(non-preemptive)
Given process, the burst time of a process respectively and a quantum limit; the task is to find and print the waiting time, turnaround time and their respective average time using Shortest Job First Scheduling non-preemptive method.
What is the shortest job first scheduling?
Shortest job first scheduling is the job or process scheduling algorithm that follows the nonpreemptive scheduling discipline. In this, scheduler selects the process from the waiting queue with the least completion time and allocate the CPU to that job or process. Shortest Job First is more desirable than FIFO algorithm because SJF is more optimal as it reduces average wait time which will increase the throughput.
What is the Turnaround time, waiting time and completion time?
- Completion Time is the time required by the process to complete its execution
Turnaround Time is the time interval between the submission of a process and its completion.
Turnaround Time = completion of a process – submission of a process
Waiting Time is the difference between turnaround time and burst time
Waiting Time = turnaround time – burst time
Example
We are given with the processes P1, P2, P3, P4 and P5 having their corresponding burst time given below
| Process | Burst Time |
|---|---|
| P1 | 4 |
| P2 | 2 |
| P3 | 8 |
| P4 | 1 |
| P5 | 9 |
Since the burst time of process P4 is minimum amongst all the processes it will be allocated CPU first. After that, P2 will be queued then P1, P3 and P5.
Average waiting time is calculated on the basis of gantt chart. P1 have to wait for 3, P2 have to wait for 1, P3 have to wait for 7, P4 have to wait for 0 and P5 have to wait for 15. So, their average waiting time will be −
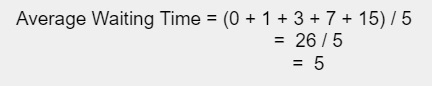
Algorithm
Start
Step 1-> In function swap(int *a, int *b)
Set temp = *a
Set *a = *b
Set *b = temp
Step 2-> In function arrangeArrival(int num, int mat[][3])
Loop For i=0 and i<num and i++
Loop For j=0 and j<num-i-1 and j++
If mat[1][j] > mat[1][j+1] then,
For k=0 and k<5 and k++
Call function swap(mat[k][j], mat[k][j+1])
Step 3-> In function completionTime(int num, int mat[][3])
Declare temp, val
Set mat[3][0] = mat[1][0] + mat[2][0]
Set mat[5][0] = mat[3][0] - mat[1][0]
Set mat[4][0] = mat[5][0] - mat[2][0]
Loop For i=1 and i<num and i++
Set temp = mat[3][i-1]
Set low = mat[2][i]
Loop For j=i and j<num and j++
If temp >= mat[1][j] && low >= mat[2][j] then,
Set low = mat[2][j]
Set val = j
Set mat[3][val] = temp + mat[2][val]
Set mat[5][val] = mat[3][val] - mat[1][val]
Set mat[4][val] = mat[5][val] - mat[2][val]
Loop For k=0; k<6; k++
Call function swap(mat[k][val], mat[k][i])
Step 4-> In function int main()
Declare and set num = 3, temp
Declare and set mat[6][3] = {1, 2, 3, 3, 6, 4, 2, 3, 4}
Print Process ID, Arrival Time, Burst Time
Loop For i=0 and i<num and i++
Print the values of mat[0][i], mat[1][i], mat[2][i]
Call function arrangeArrival(num, mat)
Call function completionTime(num, mat)
Print Process ID, Arrival Time, Burst Time, Waiting Time, Turnaround Time
Loop For i=0 and i<num and i++
Print the values of mat[0][i], mat[1][i], mat[2][i], mat[4][i], mat[5][i]
StopExample
// C++ program to implement Shortest Job first with Arrival Time
#include<iostream>
using namespace std;
void swap(int *a, int *b) {
int temp = *a;
*a = *b;
*b = temp;
}
void arrangeArrival(int num, int mat[][3]) {
for(int i=0; i<num; i++) {
for(int j=0; j<num-i-1; j++) {
if(mat[1][j] > mat[1][j+1]) {
for(int k=0; k<5; k++) {
swap(mat[k][j], mat[k][j+1]);
}
}
}
}
}
void completionTime(int num, int mat[][3]) {
int temp, val;
mat[3][0] = mat[1][0] + mat[2][0];
mat[5][0] = mat[3][0] - mat[1][0];
mat[4][0] = mat[5][0] - mat[2][0];
for(int i=1; i<num; i++) {
temp = mat[3][i-1];
int low = mat[2][i];
for(int j=i; j<num; j++) {
if(temp >= mat[1][j] && low >= mat[2][j]) {
low = mat[2][j];
val = j;
}
}
mat[3][val] = temp + mat[2][val];
mat[5][val] = mat[3][val] - mat[1][val];
mat[4][val] = mat[5][val] - mat[2][val];
for(int k=0; k<6; k++) {
swap(mat[k][val], mat[k][i]);
}
}
}
int main() {
int num = 3, temp;
int mat[6][3] = {1, 2, 3, 3, 6, 4, 2, 3, 4};
cout<<"Before Arrange...\n";
cout<<"Process ID\tArrival Time\tBurst Time\n";
for(int i=0; i<num; i++) {
cout<<mat[0][i]<<"\t\t"<<mat[1][i]<<"\t\t"<<mat[2][i]<<"\n";
}
arrangeArrival(num, mat);
completionTime(num, mat);
cout<<"Final Result...\n";
cout<<"Process ID\tArrival Time\tBurst Time\tWaiting Time\tTurnaround Time\n";
for(int i=0; i<num; i++) {
cout<<mat[0][i]<<"\t\t"<<mat[1][i]<<"\t\t"<<mat[2][i]<<"\t\t"<<mat[4][i]<<"\t\t"<<mat[5][i]<<"\n";
}
}Output
5K+ Views
