Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Program for Bisection Method
Given with the function f(x) with the numbers a and b where, f(a) * f(b) > 0 and the function f(x) should lie between a and b i.e. f(x) = [a, b]. The task is to find the value of root that lies between interval a and b in function f(x) using bisection method.
What is bisection method?
Bisection method is used to find the value of a root in the function f(x) within the given limits defined by ‘a’ and ‘b’. The root of the function can be defined as the value a such that f(a) = 0.
Example
Quadratic equation F(x) = - 8 This equation is equals to 0 when the value of x will be 2 i.e. - 8 = 0 So, root of this quadratic function F(x) will be 2.
Now, If a function f(x) is continuous in the given interval [a..b] and also, sign of f(a) ≠ sign of f(b) then there will be a value m which belongs to the interval a and b such that f(m) = 0
Value m [a..b] Such that f(m) = 0
I.e. m is the value of root which can be multiple
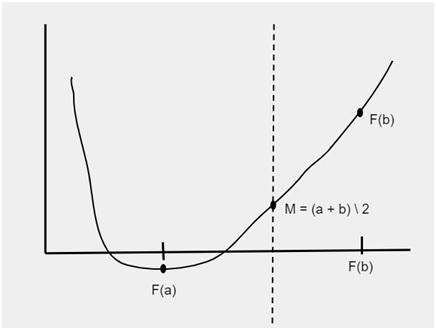
Given below is the figure which is showing the intervals f(a) and f(b). To find the root between these intervals the limit is divided into parts and stored in the variable m i.e.
m = (a + b) / 2
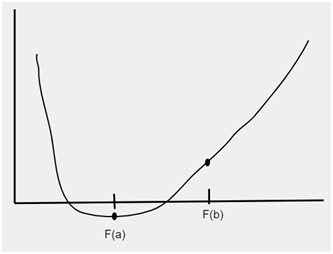
After the division of limits new interval will be generated as shown in the figure given below
Example
Input-: x^3 - x^2 + 2 ; a =-500 and b = 100 Output-: The value of root is : -0.991821 Input-: x^3 - x^2 + 2 ; a =-200 and b = 300 Output-: The value of root is : -1.0025
Approach that we are using in the below program is as follow −
- Input the equation and the value of intervals a and b
- Divide the intervals as : m = (a + b) / 2
- Print m is the root
- If f(m) ≠ 0
- Check if f(a) * f(m) < 0
- Then root will lie between a and m
- Check if f(b) * f(m) < 0
- Then root will lie between b and m
Algorithm
Start Step 1-> In function double solution(double x) Return x*x*x - x*x + 2 Step 2-> In function bisection(double a, double b) If solution(a) * solution(b) >= 0 then, Print "You have not assumed right a and b " Return End If Set c = a Loop While (b-a) >= EP Set c = (a+b)/2 If solution(c) == 0.0 Break End If Else if solution(c)*solution(a) < 0 Set b = c End Else If Else Set a = c End Else End Print "The value of root” Step 3-> In function int main() Declare and Initialize inputs a =-500, b = 100 Call function bisection(a, b) Stop
Example
#include <iostream>
using namespace std;
#define EP 0.01
// An example function whose solution is determined using
// Bisection Method. The function is x^3 - x^2 + 2
double solution(double x) {
return x*x*x - x*x + 2;
}
// Prints root of solution(x) with error in EPSILON
void bisection(double a, double b) {
if (solution(a) * solution(b) >= 0) {
cout << "You have not assumed right a and b\n";
return;
}
double c = a;
while ((b-a) >= EP) {
// Find middle point
c = (a+b)/2;
// Check if middle point is root
if (solution(c) == 0.0)
break;
// Decide the side to repeat the steps
else if (solution(c)*solution(a) < 0)
b = c;
else
a = c;
}
cout << "The value of root is : " << c;
}
// main function
int main() {
double a =-500, b = 100;
bisection(a, b);
return 0;
}Output
The value of root is : -0.991821
13K+ Views
