Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
C++ Perimeter and Area of Varignon’s Parallelogram
Varignon’s Parallelogram is formed by joining midpoints of each side of a quadrilateral. Let’s say we have a quadrilateral ABCD. The midpoints of each side are P, Q, R, and S. If we connect all the midpoints, it will always form a parallelogram PQRS known as Varignon’s Parallelogram.
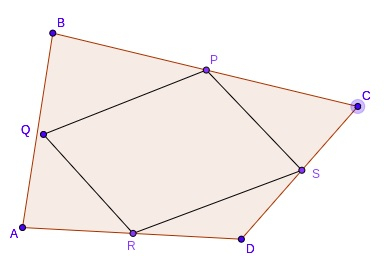
In this tutorial, we will discuss how to find the perimeter and area of Varignon’s Parallelogram with the given two diagonals and the area of a quadrilateral, for example −
Input: d1 = 6, d2 = 9, Area = 12 Output: Perimeter = 15 Area = 6 Input: d1 = 11, d2 = 13, Area = 32 Output: Perimeter = 24 Area = 16
Approach to Find the Solution
In triangle P and Q are midpoints of AB, AC respectively,
By midpoint theorem, PQ = (1/2)*AC
Similarly applying theorem to triangle ADC, RS = (1/2)*BD,
So PQ=RS=(1/2)*AC and PS=QR=(1/2)*BD
The perimeter of PQRS = AC + BD(sum of diagonals)
EF=GH=(1/2)*AC and EH=FG=(1/2)*BD
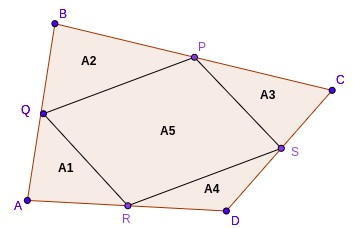
For the Area of PQRS, we divide the figure into four triangles, and areas of four triangles are,
A1=(1/4)*area of BAD
similarly, A2=(1/4)*area of ABC
A3=(1/4)*area of BCD
A4=(1/4)*area of ACD.
A1 + A2 + A3 + A4 = (1/4)*(area of triangles ACD+ABC+BCD+BAD)
= (¼) * 2* area of ABCD
= (½) * area of quad ABCD
Now A1 + A2 + A3 + A4 = (½) * area of quad ABCD
It means A5 = (½) * area of quad ABCD
So Area of parallelogram PQRS = (½) * area of quad ABCD
Now we can find the perimeter and area of PQRS by just applying the formula using C++.
Example
C++ Code for the Above Approach
#include <bits/stdc++.h>
using namespace std;
int main(){
float d1 = 6, d2 = 9, area_ABCD = 12;
float area_PQRS = area_ABCD/2;
float perimeter = d1 + d2;
cout << "Area of parallelogram PQRS = " << area_PQRS << " and perimeter = " << perimeter;
return 0;
}
Output
Area of parallelogram PQRS = 6 and perimeter = 15
Conclusion
In this tutorial, we discussed Varignon's Parallelogram and how to find the area and perimeter. We discussed the derivation of perimeter and area of a parallelogram using the midpoint theorem. We also discussed the C++ program for this problem which we can do with programming languages like C, Java, Python, etc. We hope you find this tutorial helpful.
122 Views
