Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Construct a graph from given degrees of all vertices in C++
Suppose we have a list of vertices, and their degrees are given. We have to generate one undirected graph from that degree sequence. It will not include loop or multiple edges. So if the degree sequence is like [2, 2, 1, 1], then the graph can be like
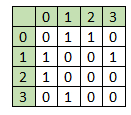
To solve this, we will follow these steps −
Define adjacency matrix adj to store the graph
for each vertex i, do
for each vertex j that is valid, and next to i
if the degree of vertex i and j are more than zero, then connect them
display the matrix.
Example
#include <iostream>
#include <iomanip>
using namespace std;
void generateGraph(int vert_degree[], int n) {
int adj_mat[n][n];
for(int i = 0; i<n; i++){
for(int j = 0; j < n; j++){
adj_mat[i][j] = 0;
}
}
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
if (vert_degree[i] > 0 && vert_degree[j] > 0) {
vert_degree[i]--; vert_degree[j]--;
adj_mat[i][j] = adj_mat[j][i] = 1;
}
}
}
cout << endl << setw(3) << " ";
for (int i = 0; i < n; i++)
cout << setw(3) << "(" << i << ")";
cout << endl << endl;
for (int i = 0; i < n; i++) {
cout << setw(4) << "(" << i << ")";
for (int j = 0; j < n; j++)
cout << setw(5) << adj_mat[i][j];
cout << endl;
}
}
int main() {
int vert_degree[] = { 2, 2, 1, 1, 1 };
int n = sizeof(vert_degree) / sizeof(vert_degree[0]);
generateGraph(vert_degree, n);
}
Output
(0) (1) (2) (3) (4) (0) 0 1 1 0 0 (1) 1 0 0 1 0 (2) 1 0 0 0 0 (3) 0 1 0 0 0 (4) 0 0 0 0 0
Updated on: 03-Jan-2020
230 Views
Advertisements