- Compiler Design - Home
- Compiler Design - Overview
- Compiler Design - Architecture
- Phases
- Compiler Design - Phases
- Compiler Design - Global Optimization
- Compiler Design - Local Optimization
- Lexical Analysis
- Compiler Design - Lexical Analysis
- Compiler Design - Regular Expressions
- Compiler Design - Finite Automata
- Compiler Design - Language Elements
- Compiler Design - Lexical Tokens
- Compiler Design - FSM
- Compiler Design - Lexical Table
- Compiler Design - Sequential Search
- Compiler Design - Binary Search Tree
- Compiler Design - Hash Table
- Syntax Analysis
- Compiler Design - Syntax Analysis
- Compiler Design - Parsing Types
- Compiler Design - Grammars
- Compiler Design - Classes Grammars
- Compiler Design - Pushdown Automata
- Compiler Design - Ambiguous Grammar
- Parsing
- Compiler Design - Top-Down Parser
- Compiler Design - Bottom-Up Parser
- Compiler Design - Simple Grammar
- Compiler Design - Quasi-Simple Grammar
- Compiler Design - LL(1) Grammar
- Error Recovery
- Compiler Design - Error Recovery
- Semantic Analysis
- Compiler Design - Semantic Analysis
- Compiler Design - Symbol Table
- Run Time
- Compiler Design - Run-time Environment
- Code Generation
- Compiler Design - Code Generation
- Converting Atoms to Instructions
- Compiler Design - Transfer of Control
- Compiler Design - Register Allocation
- Forward Transfer of Control
- Reverse Transfer of Control
- Code Optimization
- Compiler Design - Code Optimization
- Compiler Design - Intermediate Code
- Basic Blocks and DAGs
- Control Flow Graph
- Compiler Design - Peephole Optimization
- Implementing Translation Grammars
- Compiler Design - Attributed Grammars
Compiler Design - Finite Automata
Finite Automata
Finite automata is a state machine that takes a string of symbols as input and changes its state accordingly. Finite automata is a recognizer for regular expressions. When a regular expression string is fed into finite automata, it changes its state for each literal. If the input string is successfully processed and the automata reaches its final state, it is accepted, i.e., the string just fed was said to be a valid token of the language in hand.
Mathematical Model of Finite Automata
The mathematical model of finite automata consists of:
- Finite set of states (Q)
- Finite set of input symbols ()
- One Start state (q0)
- Set of final states (qf)
- Transition function ()
The transition function () maps the finite set of state (Q) to a finite set of input symbols (), Q Q
Finite Automata Construction
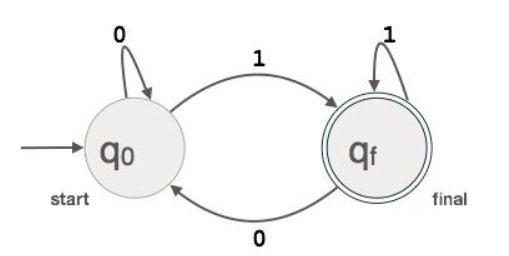
Let L(r) be a regular language recognized by some finite automata (FA).
States : States of FA are represented by circles. State names are written inside circles.
Start state : The state from where the automata starts, is known as the start state. Start state has an arrow pointed towards it.
Intermediate states : All intermediate states have at least two arrows; one pointing to and another pointing out from them.
Final state : If the input string is successfully parsed, the automata is expected to be in this state. Final state is represented by double circles. It may have any odd number of arrows pointing to it and even number of arrows pointing out from it. The number of odd arrows are one greater than even, i.e. odd = even+1.
Transition : The transition from one state to another state happens when a desired symbol in the input is found. Upon transition, automata can either move to the next state or stay in the same state. Movement from one state to another is shown as a directed arrow, where the arrows points to the destination state. If automata stays on the same state, an arrow pointing from a state to itself is drawn.
Example : We assume FA accepts any three digit binary value ending in digit 1. FA = {Q(q0, qf), (0,1), q0, qf, }