Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Check if a number can be represented as a sum of 2 triangular numbers in C++
In this section, we will see if we can express one number as the sum of two triangular numbers or not. The triangular numbers are like below −
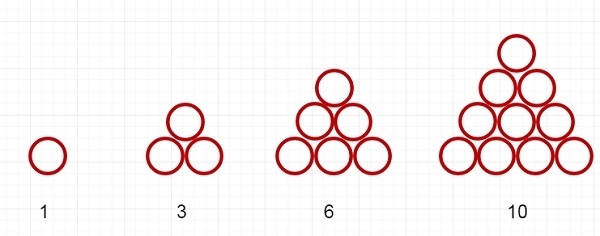
From the example, we can see that 1, 3, 6, 10 are some triangular numbers. We need to express a number N (say 16) as sum of two triangular numbers (6, 10).
The approach is very simple. We have to get all triangular numbers less than N. Form a set from these values. Now we have to take a number say X from the set, and check whether N – X is present in the set, then X can be represented as sum of two triangular numbers.
Example
#include <iostream>
#include <set>
using namespace std;
bool isSumTriangularNum(int n) {
set<int> s;
int i = 1;
while (1) { //find and store all triangular numbers below n, and store into set
int x = i * (i + 1) / 2;
if (x >= n)
break;
s.insert(x);
i++;
}
for (auto x : s)
if (s.find(n - x) != s.end())
return true;
return false;
}
int main() {
int num = 16;
if(isSumTriangularNum(num)){
cout << "Can be represented";
}else{
cout << "Cannot be represented";
}
}Output
Can be represented
Updated on: 27-Sep-2019
92 Views
Advertisements