Centers of a tree

The center of a tree is a vertex with minimal eccentricity. The eccentricity of a vertex X in a tree G is the maximum distance between the vertex X and any other vertex of the tree. The maximum eccentricity is the tree diameter. If a tree has only one center, it is called Central Tree and if a tree has only more than one centers, it is called Bi-central Tree. Every tree is either central or bi-central.

Algorithm to find centers and bi-centers of a tree

Step 1 − Remove all the vertices of degree 1 from the given tree and also remove their incident edges.

Step 2 − Repeat step 1 until either a single vertex or two vertices joined by an edge is left. If a single vertex is left then it is the center of the tree and if two vertices joined by an edge is left then it is the bi-center of the tree.

Problem 1

Find out the center/bi-center of the following tree −

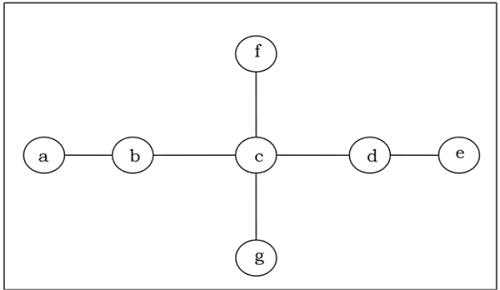
Solution

At first, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

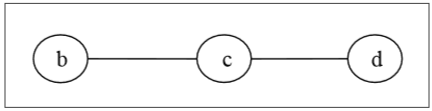
Again, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

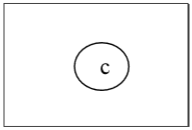
Finally we got a single vertex 'c' and we stop the algorithm. As there is single vertex, this tree has one center 'c' and the tree is a central tree.

Problem 2

Find out the center/bi-center of the following tree −

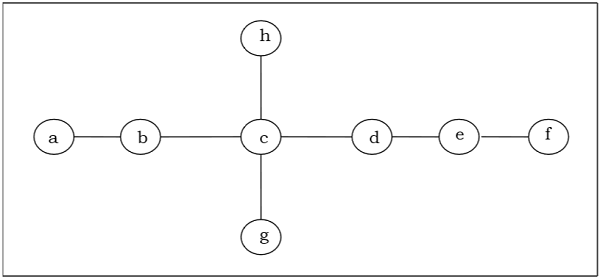
Solution

At first, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

Again, we will remove all vertices of degree 1 and also remove their incident edges and get the following tree −

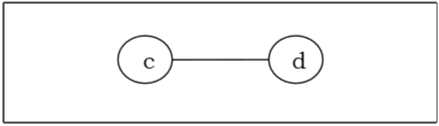
Finally, we got two vertices 'c' and 'd' left, hence we stop the algorithm. As two vertices joined by an edge is left, this tree has bi-center 'cd' and the tree is bi-central.

Mahesh Parahar

Updated on: 23-Aug-2019

3K+ Views

Kickstart Your Career

Get certified by completing the course

Get Started