Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binomial Heap in C++?
Binomial Heap is defined as an extension of Binary Heap that provides faster merge or union operation together with other operations provided by Binary Heap.
A Binomial Heap is treated as a collection of Binomial Trees.
What is a Binomial Tree?
A Binomial Tree of order k can be built by taking two binomial trees of order k-1 and treating one as leftmost child or other.
A Binomial Tree of order k has below properties.
The number of nodes of Binomial Tree has exactly 2k.
The depth of Binomial Tree is k.
There are exactly kCi nodes at depth i where i = 0, 1, . . . , k.
The root with degree k and children of root are themselves treated as Binomial Trees with order k-1, k-2,..0 from left to right.
Binomial Heap −
A Binomial Heap is defined as a set of Binomial Trees where each Binomial Tree follows Min Heap property. And having any degree, there can be maximum one Binomial Tree of any degree.
Examples Binomial Heap −
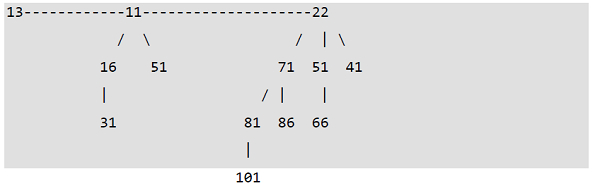
A Binomial Heap having 12 nodes. It is treated as a collection of 2
From left to right Binomial Trees of orders 2 and 3
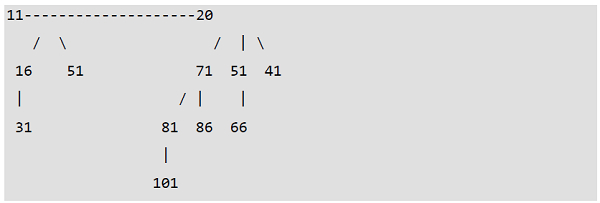
Binomial Heaps and Binary Representation of a number
A Binomial Heap having m nodes has the number of Binomial Trees equal to the number of set bits in the Binary representation of m. For example, suppose m be 13, there 3 set bits in the binary representation of m (00001101), that indicating 3 Binomial Trees. We can also be able to relate the degree of these Binomial Trees with positions of set bits. With the help of this relation, we can decide or conclude that there are O(logm) Binomial Trees in a Binomial Heap with ‘m’ nodes
Operations of Binomial Heap −
union() is the main operation in Binomial Heap, all other operations mainly implement this operation. The union() operation is responsible to combine two Binomial Heaps into one.
insert(h, K)− Inserts a key ‘K’ to Binomial Heap ‘h’. At first, this operation is able to create a Binomial Heap with single key ‘K’, then calls union on h and the new Binomial heap.
getMin(h)− A simple method to getMin() is to visit the list of root of Binomial Trees and return the smallest key.
This application requires O(logm) time. It can be improved to O(1) by maintaining a pointer to smallest key root.
extractMin(h)− This operation also implements union(). At first, we call getMin() to calculate the smallest key Binomial Tree, next we remove the node and create a new Binomial Heap by combining all subtrees of the removed smallest node. At last, we call union() on h as well as the newly created Binomial Heap. This operation requires O(logm) time.
delete(h)− Same as Binary Heap, at first, delete operation reduces the key to minus infinite, next calls extractMin().
decreaseKey(h)− decreaseKey() is also same as Binary Heap. At first, we compare the decreases key with it parent and if parent’s key is more, then we exchange keys and recur for the parent. At last, we stop when we either reach a node whose parent has a smaller key or we arrive the root node. Time complexity of decreaseKey() is O(logm).
311 Views
