Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Binary Tree with Array implementation in C++
A binary tree is a special type of tree in which each node of the tree can have at most two child nodes. These child nodes are known as right child and left child.
A simple binary tree is −
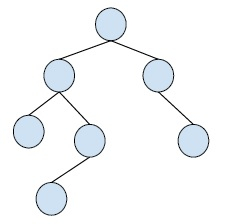
For representing trees, there are two ways,
- dynamic node representation which uses linked list
- Sequential representation which uses array.
Here, we will discuss about array representation of binary tree. For this we need to number the nodes of the BT. This numbering can start from 0 to (n-1) or from 1 to n.
Lets derive the positions of nodes and their parent and child nodes in the array.
When we use 0 index based sequencing,
Suppose parent node is an index p.
Then, the left_child node is at index (2*p)+ 1.
The right_child node is at index (2*p) + 2.
Root node is at index 0.
left_child is at index 1.
Right_child is at index 2.
When we use 1 index based sequencing,
Suppose parent node is at index p,
Right_node is at index (2*p).
Left_node is at index (2*p)+1.
Root node is at index 1.
left_child is at index 2.
Right_child is at index 3.
Example
#include<bits/stdc++.h>
using namespace std;
char tree[10];
int rootnode(char key){
if(tree[0] != '\0')
cout<<"Tree already had root";
else
tree[0] = key;
return 0;
}
int leftchild(char key, int parent){
if(tree[parent] == '\0')
cout <<"\nCan't set child at"<<(parent * 2) + 1<<" , no parent found";
else
tree[(parent * 2) + 1] = key;
return 0;
}
int rightchild(char key, int parent){
if(tree[parent] == '\0')
cout<<"\nCan't set child at"<<(parent * 2) + 2<<" , no parent found";
else
tree[(parent * 2) + 2] = key;
return 0;
}
int traversetree(){
cout << "\n";
for(int i = 0; i < 10; i++){
if(tree[i] != '\0')
cout<<tree[i];
else
cout<<"-";
}
return 0;
}
int main(){
rootnode('A');
rightchild('C', 2);
leftchild('D', 0);
rightchild('E', 1);
rightchild('F', 2);
traversetree();
return 0;
}Output
Can't set child at6 , no parent found Can't set child at6 , no parent found AD--E-----
4K+ Views
