Data Structure
Data Structure Networking
Networking RDBMS
RDBMS Operating System
Operating System Java
Java MS Excel
MS Excel iOS
iOS HTML
HTML CSS
CSS Android
Android Python
Python C Programming
C Programming C++
C++ C#
C# MongoDB
MongoDB MySQL
MySQL Javascript
Javascript PHP
PHP
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
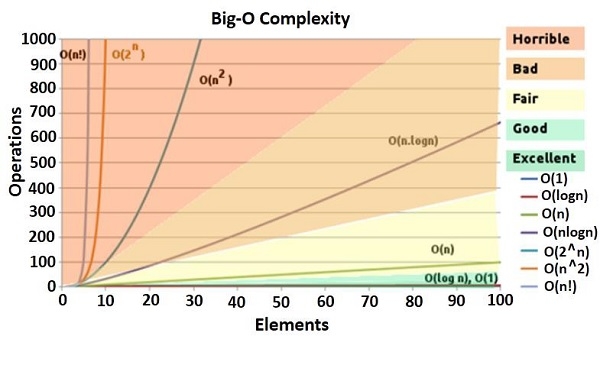
Asymptotic Complexity
Asymptotic Analysis
Using asymptotic analysis, we can get an idea about the performance of the algorithm based on the input size. We should not calculate the exact running time, but we should find the relation between the running time and the input size. We should follow the running time when the size of input is increased.
For the space complexity, our goal is to get the relation or function that how much space in the main memory is occupied to complete the algorithm.
Asymptotic Behavior
For a function f(n) the asymptotic behavior is the growth of f(n) as n gets large. Small input values are not considered. Our task is to find how much time it will take for large value of the input.
For example, f(n) = c * n + k as linear time complexity. f(n) = c * n2 + k is quadratic time complexity.
The analysis of algorithms can be divided into three different cases. The cases are as follows −
Best Case − Here the lower bound of running time is calculated. It describes the behavior of algorithm under optimal conditions.
Average Case − In this case we calculate the region between upper and lower bound of the running time of algorithms. In this case the number of executed operations are not minimum and not maximum.
Worst Case − In this case we calculate the upper bound of the running time of algorithms. In this case maximum number of operations are executed.