
- Angles, Lines, and Polygons
- Home
- Measuring an angle with the protractor
- Acute, obtuse, and right angles
- Naming segments, rays, and lines
- Identifying parallel and perpendicular lines
- Acute, obtuse, and right triangles
- Classifying scalene, isosceles, and equilateral triangles by side lengths or angles
- Finding an angle measure of a triangle given two angles
- Naming polygons
- Drawing and identifying a polygon in the coordinate plane
Identifying parallel and perpendicular lines
Definitions
Parallel lines − If two lines are equidistant from each other extending indefinitely in both directions, then they are said to be parallel to each other. Parallel lines do not intersect each other.
Perpendicular lines − If two lines intersect each other at right angles, they are called perpendicular lines.
Rules to identify parallel and perpendicular lines
When identifying parallel lines we see if the two lines are equidistant from each other and if this condition is satisfied, they are parallel to each other and they are parallel lines.
When identifying perpendicular lines, we first see if the lines intersect. If the lines intersect, we see if they intersect at right angles. Then they are perpendicular to each other and are perpendicular lines.
Example 1
Use parallel or perpendicular to describe the following lines.
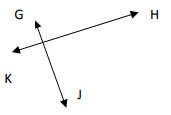
Solution
Step 1:
Given lines intersect each other at right angles. They are perpendicular to each other.
Step 2:
So the given lines are perpendicular lines.
Example 2
Use parallel or perpendicular to describe the following lines.
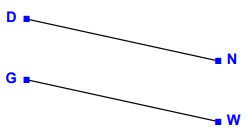
Solution
Step 1:
Given lines do not intersect and are equidistant from each other. They are parallel to each other.
Step 2:
So the given lines are parallel lines.