Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Add all greater values to every node in the given BST
Here we will see one interesting problem, where we will add greater values to every node in one given binary search tree. So the initial and final tree will be look like below −
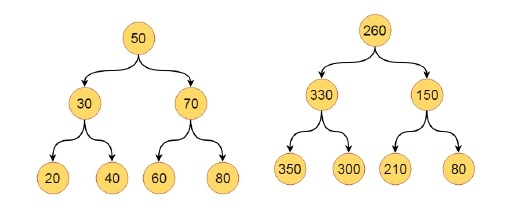
Algorithm
bstUpdate(root, sum) −
Begin if root is null, then stop bstUpdate(right of room, sum) sum := sum + value of root update root value using sum bstUpdate(left of room, sum) End
Example
#include<iostream>
using namespace std;
class Node {
public:
int data;
Node *left, *right;
};
Node *getNode(int item) {
Node *newNode = new Node();
newNode->data = item;
newNode->left = newNode->right = NULL;
return newNode;
}
void updateBST(Node *root, int *sum) {
if (root == NULL)
return;
updateBST(root->right, sum); //update right sub tree
*sum = *sum + root->data;
root->data = *sum; //update root data
updateBST(root->left, sum); //update left sub tree
}
void BSTUpdate(Node *root) {
int sum = 0;
updateBST(root, &sum);
}
void inorder(Node *root) {
if (root != NULL) {
inorder(root->left);
cout<<root->data<<" ";
inorder(root->right);
}
}
Node* insert(Node* node, int data) {
if (node == NULL)
return getNode(data);
if (data <= node->data) //go to left
node->left = insert(node->left, data);
else //go to right
node->right = insert(node->right, data);
return node;
}
int main() {
int data[] = {50, 30, 20, 40, 70, 60, 80};
int n = sizeof(data)/sizeof(data[0]);
Node *root = NULL;
for(int i = 0; i < n; i++) {
root = insert(root, data[i]);
}
BSTUpdate(root);
inorder(root);
}Output
350 330 300 260 210 150 80
Updated on: 20-Aug-2019
69 Views
Advertisements