Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Topological Sorting
The topological sorting for a directed acyclic graph is the linear ordering of vertices. For every edge U-V of a directed graph, the vertex u will come before vertex v in the ordering.
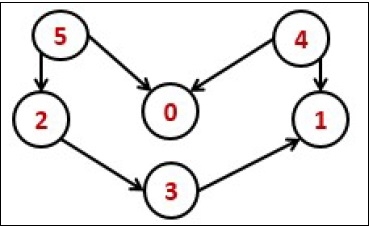
As we know that the source vertex will come after the destination vertex, so we need to use a stack to store previous elements. After completing all nodes, we can simply display them from the stack.
Input and Output
Input: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 0 0 1 0 1 0 0 0 Output: Nodes after topological sorted order: 5 4 2 3 1 0
Algorithm
topoSort(u, visited, stack)
Input − The start vertex u, An array to keep track of which node is visited or not. A stack to store nodes.
Output − Sorting the vertices in topological sequence in the stack.
Begin mark u as visited for all vertices v which is adjacent with u, do if v is not visited, then topoSort(c, visited, stack) done push u into a stack End
performTopologicalSorting(Graph)
Input − The given directed acyclic graph.
Output − Sequence of nodes.
Begin initially mark all nodes as unvisited for all nodes v of the graph, do if v is not visited, then topoSort(i, visited, stack) done pop and print all elements from the stack End.
Example
#include<iostream>
#include<stack>
#define NODE 6
using namespace std;
int graph[NODE][NODE] = {
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 0, 0, 0},
{0, 0, 0, 1, 0, 0},
{0, 1, 0, 0, 0, 0},
{1, 1, 0, 0, 0, 0},
{1, 0, 1, 0, 0, 0}
};
void topoSort(int u, bool visited[], stack<int>&stk) {
visited[u] = true; //set as the node v is visited
for(int v = 0; v<NODE; v++) {
if(graph[u][v]) { //for allvertices v adjacent to u
if(!visited[v])
topoSort(v, visited, stk);
}
}
stk.push(u); //push starting vertex into the stack
}
void performTopologicalSort() {
stack<int> stk;
bool vis[NODE];
for(int i = 0; i<NODE; i++)
vis[i] = false; //initially all nodes are unvisited
for(int i = 0; i<NODE; i++)
if(!vis[i]) //when node is not visited
topoSort(i, vis, stk);
while(!stk.empty()) {
cout << stk.top() << " ";
stk.pop();
}
}
main() {
cout << "Nodes after topological sorted order: ";
performTopologicalSort();
}Output
Nodes after topological sorted order: 5 4 2 3 1 0
Updated on: 16-Jun-2020
5K+ Views
Advertisements