Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Snake and Ladder Problem
We know about the famous game Snake and Ladder. In this game, some rooms are present on the board, with the room number. Some rooms are connected with a ladder or with snakes. When we get a ladder, we can climb up to some rooms to reach near to the destination without moving sequentially. Similarly, when we get some snake, it sends us to a lower room to start the journey again from that room.
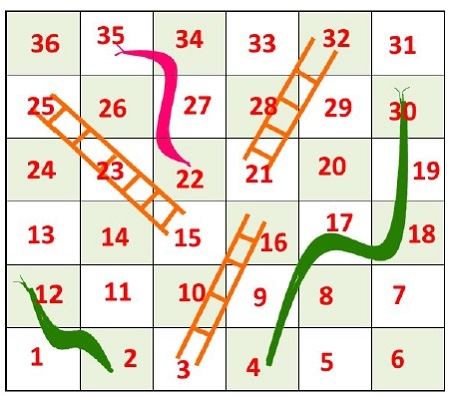
In this problem, we have to find the minimum number of the dice throw is required to reach start to destination.
Input and Output
Input: The starting and ending location of the snake and ladders. Snake: From 26 to 0, From 20 to 8, From 16 to 3, From 18 to 6 Ladder From 2 to 21, From 4 to 7, From 10 to 25, from 19 to 28 Output: Min Dice throws required is 3
Algorithm
minDiceThrow(move, cell)
Input: jump location for snake or ladder, and the total number of cells.
Output: Minimum number of dice throw required to reach to the final cell.
Begin initially mark all cell as unvisited define queue q mark the staring vertex as visited for starting vertex the vertex number := 0 and distance := 0 add starting vertex s into q while q is not empty, do qVert := front element of the queue v := vertex number of qVert if v = cell -1, then //when it is last vertex break the loop delete one item from queue for j := v + 1, to v + 6 and j < cell, increase j by 1, do if j is not visited, then newVert.dist := (qVert.dist + 1) mark v as visited if there is snake or ladder, then newVert.vert := move[j] //jump to that location else newVert.vert := j insert newVert into queue done done return qVert.dist End
Example
#include<iostream>
#include <queue>
using namespace std;
struct vertex {
int vert;
int dist; // Distance of this vertex from source
};
int minDiceThrow(int move[], int cell) {
bool visited[cell];
for (int i = 0; i < cell; i++)
visited[i] = false; //initially all cells are unvisited
queue<vertex> q;
visited[0] = true; //initially starting from 0
vertex s = {0, 0};
q.push(s); // Enqueue 0'th vertex
vertex qVert;
while (!q.empty()) {
qVert = q.front();
int v = qVert.vert;
if (v == cell-1) //when v is the destination vertex
break;
q.pop();
for (int j=v+1; j<=(v+6) && j<cell; ++j) { //for next 1 to 6 cells
if (!visited[j]) {
vertex newVert;
newVert.dist = (qVert.dist + 1); //initially distance increased by 1
visited[j] = true;
if (move[j] != -1)
newVert.vert = move[j]; //if jth place have snake or ladder
else
newVert.vert = j;
q.push(newVert);
}
}
}
return qVert.dist; //number of minimum dice throw
}
int main() {
int cell = 30; //consider there are 30 cells
int moves[cell];
for (int i = 0; i<cell; i++)
moves[i] = -1; //initially no snake or ladder are initialized
//For ladder in cell i, it jumps to move[i]
moves[2] = 21;
moves[4] = 7;
moves[10] = 25;
moves[19] = 28;
//For snake in cell i, it jumps to move[i]
moves[26] = 0;
moves[20] = 8;
moves[16] = 3;
moves[18] = 6;
cout << "Min Dice throws required is " << minDiceThrow(moves, cell);
}Output
Min Dice throws required is 3
Updated on: 16-Jun-2020
1K+ Views
Advertisements