Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Runge-Kutta 4th order rule for differential equation
Runge Kutta method is used for solving ordinary differential equations (ODE). It uses dy/dx function for x and y, and also need the initial value of y, i.e. y(0). It finds the approximate value of y for given x. For solving ODE, we have to follow these formulas:
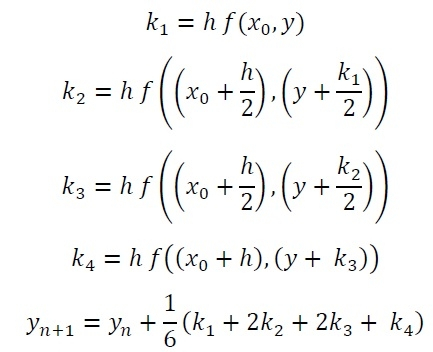
Here h is the height of the interval.
Note: From these formulas, we can use first two k1 and k2 find the Runge-Kutta 2nd Order solution for ODE.
Input and Output
Input: The x0 and f(x0): 0 and 0 the value of x = 0.4 the value of h = 0.1 Output: Answer of differential equation: 0.0213594
Algorithm
rungeKutta(x0, y0, x, h)
Input − Initial x and y value, the targeted x value, and the height of interval h.
Output − The value of y for value x.
Begin iteration := (x – x0)/h y = y0 for i := 1 to iteration, do k1 := h*f(x0, y) k2 := h*f((x0 + h/2), (y + k1/2)) k3 := h*f((x0 + h/2), (y + k2/2)) k4 := h*f((x0 + h), (y + k3)) y := y + (1/6)*(k1 + 2k2 + 2k3 + k4) x0 := x0 + h done return y End
Example
#include <iostream>
using namespace std;
double diffOfy(double x, double y) {
return ((x*x)+(y*y)); //function x^2 + y^2
}
double rk4thOrder(double x0, double y0, double x, double h) {
int iteration = int((x - x0)/h); //calculate number of iterations
double k1, k2, k3, k4;
double y = y0; //initially y is f(x0)
for(int i = 1; i<=iteration; i++) {
k1 = h*diffOfy(x0, y);
k2 = h*diffOfy((x0+h/2), (y+k1/2));
k3 = h*diffOfy((x0+h/2), (y+k2/2));
k4 = h*diffOfy((x0+h), (y+k3));
y += double((1.0/6.0)*(k1+2*k2+2*k3+k4)); //update y using del y
x0 += h; //update x0 by h
}
return y; //f(x) value
}
int main() {
double x0, y0, x, h;
cout << "Enter x0 and f(x0): "; cin >> x0 >> y0;
cout << "Enter x: "; cin >> x;
cout << "Enter h: "; cin >> h;
cout << "Answer of differential equation: " << rk4thOrder(x0, y0, x, h);
}Output
Enter x0 and f(x0): 0 0 Enter x: 0.4 Enter h: 0.1 Answer of differential equation: 0.0213594
Updated on: 17-Jun-2020
2K+ Views
Advertisements