Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Minimum Initial Points to Reach Destination
To start from the top-left corner of a given grid, one has to reach the bottom-right corner. Each cell in the grid contains a number, the number may positive or negative. When the person reaches a cell (i, j) the number of tokens he has, may be increased or decreased along with the values of that cell. We have to find the minimum number of initial tokens are required to complete the journey.
There are some rules −
- We can either move to the right or to the bottom.
- We cannot move to a cell (i, j) if our total token is less the value of (i, j).
- We have to reach the destination with minimum positive points.
Input and Output
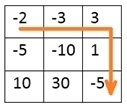
Input: The token for each room as a matrix. -2 -3 3 -5 -10 1 10 30 -5 Output: The minimum token required to start the journey. For this example, the required token is 7.
Algorithm
minInitTokens(matrix)
Input: The token matrix for each room.
Output − minimum token required to reach start point to the destination.
Begin define matrix minToken of size same as matrix m := number of rows in matrix n := number of columns in matrix if matrix[m-1, n-1] > 0, then minToken[m-1, n-1] := 0 else minToken[m-1, n-1] := 1 + absolute value of matrix[m-1, n-1] for i := m-2 down to 0, do minToken[i, n-1] := maximum of 1 and (minToken[i+1, n-1]-matrix[i,n-1]) done for j := n-2 down to 0, do minToken[m-1, j] := maximum of 1 and (minToken[m-1, j+1]-matrix[m-1, j]) done for i := m-2 down to 0, do for j := n-2 down to 0, do rem := minimum of minToken[i+1, j] and minToken[i, j+1] minPoint[i, j] := maximum of 1 and (rem – matrix[i,j]) done done return minToken[0, 0] End
Example
#include<iostream>
#include<cmath>
#define ROW 3
#define COL 3
using namespace std;
int tokens[ROW][COL] = {
{-2,-3,3},
{-5,-10,1},
{10,30,-5}
};
int max(int a, int b) {
return (a>b)?a:b;
}
int minInitPoints() {
int minToken[ROW][COL];
int m = ROW, n = COL;
minToken[m-1][n-1] = tokens[m-1][n-1] > 0? 1: abs(tokens[m-1][n-1]) + 1;
for (int i = m-2; i >= 0; i--) //from last row to first row, fill points
minToken[i][n-1] = max(minToken[i+1][n-1] - tokens[i][n-1], 1);
for (int j = n-2; j >= 0; j--) //fill last column to first column, fill points
minToken[m-1][j] = max(minToken[m-1][j+1] - tokens[m-1][j], 1);
for (int i=m-2; i>=0; i--) {
for (int j=n-2; j>=0; j--) {
int remPoint = min(minToken[i+1][j], minToken[i][j+1]); //calculate remaining points
minToken[i][j] = max(remPoint - tokens[i][j], 1);
}
}
return minToken[0][0];
}
int main() {
cout << "Minimum Points Required: " << minInitPoints();
}Output
Minimum Points Required: 7
Updated on: 17-Jun-2020
685 Views
Advertisements