Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Min Cost Path
A matrix of the different cost is given. Also, the destination cell is provided. We have to find minimum cost path to reach the destination cell from the starting cell (0, 0).
Each cell of the matrix represents the cost to traverse through that cell.
From a cell, we cannot move anywhere, we can move either to the right or to the bottom or to the lower right diagonal cell, to reach the destination.
Input and Output
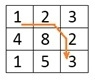
Input: The cost matrix. And the destination point. In this case the destination point is (2, 2). 1 2 3 4 8 2 1 5 3 Output: The minimum cost to reach to the destination from (0, 0). The minimum cost is 8.
Algorithm
minCostPath(destX, destY, cost)
Input − The (x, y) place of the destination, and the cost matrix.
Output − Minimum cost to reach a destination.
Begin define matrix totalCost, whose order is same as cost matrix totalCost[0, 0] = cost[0, 0] for i := 1 to destX, do totalCost[i, 0] := totalCost[i-1, 0] + cost[i, 0] done for j := 1 to destY, do totalCost[0, j] := totalCost[0, j-1] + cost[0, j] done for all places (i, j) from (1, 1) to (destX, destY), do totalCost[i, j] := minimum of totalCost[i-1, j-1], totalCost[i-1, j] and (totalCost[i, j-1] + cost[i,j]) done return totalCost[destX, destY] End
Example
#include<iostream>
#define ROW 3
#define COL 3
using namespace std;
int cost[ROW][COL] = {
{1, 2, 3},
{4, 8, 2},
{1, 5, 3}
};
int min(int a, int b, int c) {
return (a<b)?((a<c)?a:c):((b<c)?b:c);
}
int minCostPath(int destX, int destY) {
int totalCost[ROW][COL];
totalCost[0][0] = cost[0][0];
for (int i = 1; i <= destX; i++)
totalCost[i][0] = totalCost[i-1][0] + cost[i][0]; //set first col of totalCost array
for (int j = 1; j <= destY; j++) //set first row of totalCost array
totalCost[0][j] = totalCost[0][j-1] + cost[0][j];
for (int i = 1; i <= destX; i++) //for second row and column to all
for (int j = 1; j <= destY; j++)
totalCost[i][j] = min(totalCost[i-1][j-1], totalCost[i- 1][j], totalCost[i][j-1]) + cost[i][j];
return totalCost[destX][destY];
}
int main() {
cout << "Minimum Cost: "<< minCostPath(2, 2); //destination (2, 2)
return 0;
}Output
Minimum Cost: 8
Updated on: 17-Jun-2020
446 Views
Advertisements