Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
How to find if a graph is Bipartite?
A graph is said to be a bipartite graph, when vertices of that graph can be divided into two independent sets such that every edge in the graph is either start from the first set and ended in the second set, or starts from the second set, connected to the first set, in other words, we can say that no edge can found in the same set.
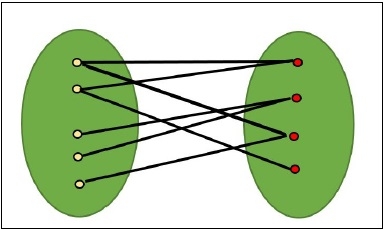
Checking of a bipartite graph is possible by using the vertex coloring. When a vertex is in the same set, it has the same color, for another set, the color will change.
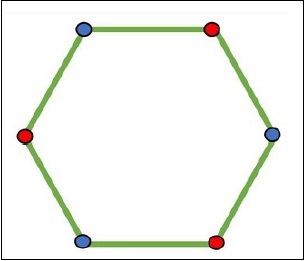
Input and Output
Input: The adjacency matrix. 0 1 1 1 0 0 1 0 0 1 1 0 1 0 0 1 0 1 1 1 1 0 1 1 0 1 0 1 0 1 0 0 1 1 1 0 Output: The graph is bipartite.
Algorithm
isBipartite(source)
Input − The source vertex.
Output: True when the graph is bipartite.
Begin define an empty queue qu, and a color list coloArray initially any node is not colored with any color color the source vertex as color red add source in the qu when qu is not empty, do remove item from the qu and take in u if there is any self-loop, then return false for all vertices v, which is connected with u, do if v has no color, then if colorArray[u] = red, then colorArray[v] := blue else if colorArray[u] = blue, then colorArray[v] := red add v into the queue if colorArray[v] = colorArray[u], then return false done done return true End
Example
#include<iostream>
#include<string>
#include<queue>
#define NODE 6
using namespace std;
/*int graph[NODE][NODE] = {
{0, 1, 1, 1, 0, 0},
{1, 0, 0, 1, 1, 0},
{1, 0, 0, 1, 0, 1},
{1, 1, 1, 0, 1, 1},
{0, 1, 0, 1, 0, 1},
{0, 0, 1, 1, 1, 0}
}; */
int graph[NODE][NODE] = {
{0, 1, 0, 0, 0, 1},
{1, 0, 1, 0, 0, 0},
{0, 1, 0, 1, 0, 0},
{0, 0, 1, 0, 1, 0},
{0, 0, 0, 1, 0, 1},
{1, 0, 0, 0, 1, 0}
};
bool isBipartite(int source) {
queue<int> qu;
string colorArray[NODE];
for(int i = 0; i< NODE; i++)
colorArray[i] = "No Color"; //initially no color is set for all vertices
colorArray[source] = "Red"; //assign red with the source vertex
qu.push(source); //add source into the queue.
while(!qu.empty()) {
int u = qu.front();
qu.pop();
if(graph[u][u] == 1) //there is a self loop
return false;
for(int v = 0; v < NODE; v++) {
if(graph[u][v] != 0 && colorArray[v] == "No Color") {
if(colorArray[u] == "Red") //assign adjacent list with alternate color
colorArray[v] = "Blue";
else if(colorArray[u] == "Blue")
colorArray[v] = "Red";
qu.push(v); //new adjacent node added to queue
} else if(graph[u][v] != 0 && colorArray[v] == colorArray[u]) {
return false; //when u and adjacent are of same color.
}
}
}
return true;
}
int main() {
bool check;
check = isBipartite(0);
if(check)
cout << "The graph is bipartite." << endl;
else
cout << "The graph is not bipartite." << endl;
} Output
The graph is bipartite.
Updated on: 16-Jun-2020
4K+ Views
Advertisements