Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Fastest Way to multiply two Numbers
Two numbers are given as a binary string, our task is to find the result of multiplication for those numbers in a faster and efficient way.
Using the Divide and Conquer strategy, we can solve the problem, in a very efficient manner. We will split the numbers into two halves.
let Xleft and Xright are two parts of first number X, and Yleft, Yright are two parts of second number Y. So the product;
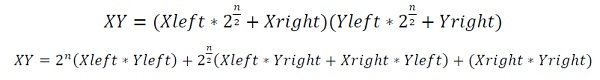
To make it simple, we can perform this operation
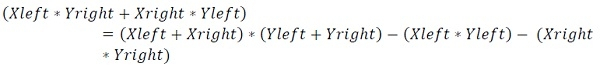
Input and Output
Input: Two binary numbers: 1101 and 0111 Output: The result is: 91
Algorithm
addBitString(num1, num2)
Input: Two numbers to add.
Output: The result after addition.
Begin adjust num1 and num2 lengths length := length of num1 carry := 0 for i := length -1 down to 0, do num1Bit := num1[i] num2Bit := num2[i] sum := num1Bit XOR num2Bit XOR carry finalSum := sum + finalSum carry := (num1Bit AND num2Bit) OR (num2Bit AND carry) OR (num1Bit AND carry) done if carry ≠ 0, then finalSum := 1 + finalSum return finalSum End
multiply(num1, num2)
Input: Two numbers to multiply.
Output: The result after multiplication.
Begin adjust num1 and num2 lengths length := length of num1 if n = 0, then return 0 if n = 1, then return (num1[0] * num2[0]) firstHalf := n/2 secondHalf := (n - firstHalf) n1Left := substring of (0 to firstHalf) from num1 n1Right := substring of (firstHalf to secondHalf) from num1 n2Left := substring of (0 to firstHalf) from num2 n2Right := substring of (firstHalf to secondHalf) from num2 p1 := multiply(n1Left, n2Left) p2 := multiply(n1Right, n2Right) add1 := addBitString(n1Left, n1Right) add2 := addBitString(n2Left, n2Right) p3 := multiply(add1, add2) mask1 := shift 1 to left for 2*secondHalf bits mask2 := shift 1 to left for secondHalf bits return P1*mask2 + (p3 – p1 – p2)*mask2 + p2 End
Example
#include<iostream>
using namespace std;
int lengthAdjust(string &num1, string &num2) { //adjust length of binary string and send length of string
int len1 = num1.size();
int len2 = num2.size();
if (len1 < len2) {
for (int i = 0 ; i < len2 - len1 ; i++)
num1 = '0' + num1; //add 0 before the first string
} else if (len1 > len2) {
for (int i = 0 ; i < len1 - len2 ; i++)
num2 = '0' + num2; //add 0 before the second string
}
return num1.size();
}
string addBitStrings(string num1, string num2) {
string finalSum;
int length = lengthAdjust(num1, num2); //adjust and update number lengths and store length
int carry = 0; // Initialize carry
for (int i = length-1 ; i >= 0 ; i--) {
int num1Bit = num1[i] - '0';
int num2Bit = num2[i] - '0';
int sum = (num1Bit ^ num2Bit ^ carry)+'0'; //we know sum = A XOR B XOR C
finalSum = (char)sum + finalSum;
//the carry = (A AND B) OR (B AND C) OR (C AND A)
carry = (num1Bit&num2Bit) | (num2Bit&carry) | (num1Bit&carry);
}
if (carry) //when carry is present
finalSum = '1' + finalSum; //add carry as MSb
return finalSum;
}
long int multiply(string num1, string num2) {
int n = lengthAdjust(num1, num2); //find length after adjusting them
if (n == 0) //when there is 0 length string, return 0
return 0;
if (n == 1)
return (num1[0] - '0')*(num2[0] - '0'); //perform single bit muliplication
int firstHalf = n/2; // First half range
int secondHalf = (n-firstHalf); // Second half range
string num1Left = num1.substr(0, firstHalf); //first half of number 1
string num1Right = num1.substr(firstHalf, secondHalf); //second half of number 1
string num2Left = num2.substr(0, firstHalf);
string num2Right = num2.substr(firstHalf, secondHalf);
// find left right multiplication, and multiply after adding left and right part
long int P1 = multiply(num1Left, num2Left);
long int P2 = multiply(num1Right, num2Right);
long int P3 = multiply(addBitStrings(num1Left, num1Right), addBitStrings(num2Left, num2Right));
return P1*(1<<(2*secondHalf)) + (P3 - P1 - P2)*(1<<secondHalf) + P2;
}
int main() {
string num1, num2;
cout << "Enter First number in Binary: "; cin >>num1;
cout << "Enter Second number in Binary: "; cin >>num2;
cout << "The result is: " << multiply(num1, num2);
}Output
Enter First number in Binary: 1101 Enter Second number in Binary: 0111 The result is: 91
Updated on: 17-Jun-2020
472 Views
Advertisements