Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
AVL Rotations in Javascript
To balance itself, an AVL tree may perform the following four kinds of rotations −
- Left rotation
- Right rotation
- Left-Right rotation
- Right-Left rotation
The first two rotations are single rotations and the next two rotations are double rotations. To have an unbalanced tree, we at least need a tree of height 2. With this simple tree, let's understand them one by one.
Left Rotation
If a tree becomes unbalanced, when a node is inserted into the right subtree of the right subtree, then we perform a single left rotation −
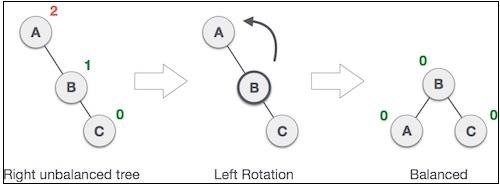
In our example, node A has become unbalanced as a node is inserted in the right subtree of A's right subtree. We perform the left rotation by making A the left-subtree of B. This rotation is also called an LL rotation. Let us look at how we can implement it −
function rotationLL(node) {
let tmp = node.left;
node.left = tmp.right;
tmp.right = node;
return tmp;
}Right Rotation
AVL tree may become unbalanced if a node is inserted in the left subtree of the left subtree. The tree then needs a right rotation.
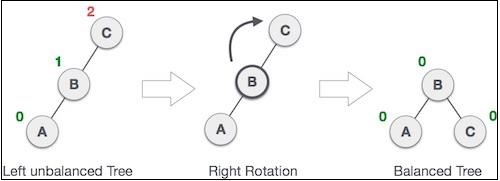
As depicted, the unbalanced node becomes the right child of its left child by performing a right rotation. This is also called an RR rotation. Let us see how it looks in code −
function rotationRR(node) {
let tmp = node.right;
node.right = tmp.left;
tmp.left = node;
return tmp;
}Left-Right Rotation
Double rotations are a slightly complex version of already explained versions of rotations. To understand them better, we should take note of each action performed while rotation. Let's first check how to perform the Left-Right rotation. A left-right rotation is a combination of left rotation followed by a right rotation.
| State | Action |
|---|---|
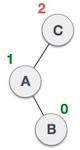 | A node has been inserted into the right subtree of the left subtree. This makes C an unbalanced node. These scenarios cause AVL tree to perform the left-right rotation. |
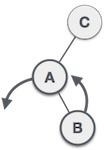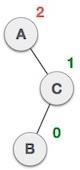
 | We first perform the left rotation on the left subtree of C. This makes A, the left subtree of B. |
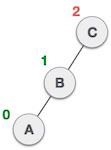 | Node C is still unbalanced, however now, it is because of the left-subtree of the left-subtree. |
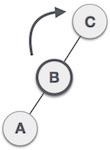 | We shall now right-rotate the tree, making B the new root node of this subtree. C now becomes the right subtree of its own left subtree. |
 | The tree is now balanced. |
This is also called an LR rotation as we first perform a left rotation followed by a right rotation. This can be implemented using the previous 2 methods as follows −
function rotationLR(node) {
node.left = rotationRR(node.left);
return rotationLL(node);
}Right-Left Rotation
The second type of double rotation is Right-Left Rotation. It is a combination of right rotation followed by a left rotation.
| State | Action |
|---|---|
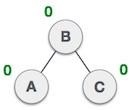
 | A node has been inserted into the left subtree of the right subtree. This makes A, an unbalanced node with balance factor 2. |
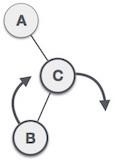 | First, we perform the right rotation along C node, making C the right subtree of its own left subtree B. Now, B becomes the right subtree of A. |
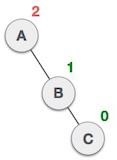 | Node A is still unbalanced because of the right subtree of its right subtree and requires a left rotation. |
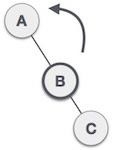 | A left rotation is performed by making B the new root node of the subtree. A becomes the left subtree of its right subtree B. |
| The tree is now balanced. |
This is also called an RL rotation as we first perform a right rotation followed by a left rotation. This can be implemented using the previous 2 methods as follows −
function rotationRL(node) {
node.right = rotationLL(node.right);
return rotationRR(node);
}
215 Views
