TensorFlow - Quick Guide

TensorFlow - Introduction

TensorFlow is a software library or framework, designed by the Google team to implement machine learning and deep learning concepts in the easiest manner. It combines the computational algebra of optimization techniques for easy calculation of many mathematical expressions.

The official website of TensorFlow is mentioned below −

www.tensorflow.org

Let us now consider the following important features of TensorFlow −

It includes a feature of that defines, optimizes and calculates mathematical expressions easily with the help of multi-dimensional arrays called tensors.
It includes a programming support of deep neural networks and machine learning techniques.
It includes a high scalable feature of computation with various data sets.
TensorFlow uses GPU computing, automating management. It also includes a unique feature of optimization of same memory and the data used.

Why is TensorFlow So Popular?

TensorFlow is well-documented and includes plenty of machine learning libraries. It offers a few important functionalities and methods for the same.

TensorFlow is also called a “Google” product. It includes a variety of machine learning and deep learning algorithms. TensorFlow can train and run deep neural networks for handwritten digit classification, image recognition, word embedding and creation of various sequence models.

TensorFlow - Installation

To install TensorFlow, it is important to have “Python” installed in your system. Python version 3.4+ is considered the best to start with TensorFlow installation.

Consider the following steps to install TensorFlow in Windows operating system.

Step 1 − Verify the python version being installed.

Step 2 − A user can pick up any mechanism to install TensorFlow in the system. We recommend “pip” and “Anaconda”. Pip is a command used for executing and installing modules in Python.

Before we install TensorFlow, we need to install Anaconda framework in our system.

After successful installation, check in command prompt through “conda” command. The execution of command is displayed below −

Step 3 − Execute the following command to initialize the installation of TensorFlow −

conda create --name tensorflow python = 3.5

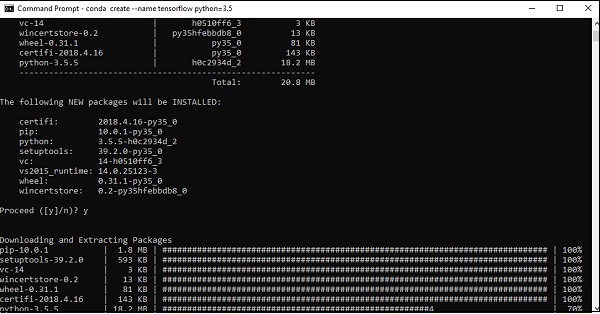
It downloads the necessary packages needed for TensorFlow setup.

Step 4 − After successful environmental setup, it is important to activate TensorFlow module.

activate tensorflow

Step 5 − Use pip to install “Tensorflow” in the system. The command used for installation is mentioned as below −

pip install tensorflow

And,

pip install tensorflow-gpu

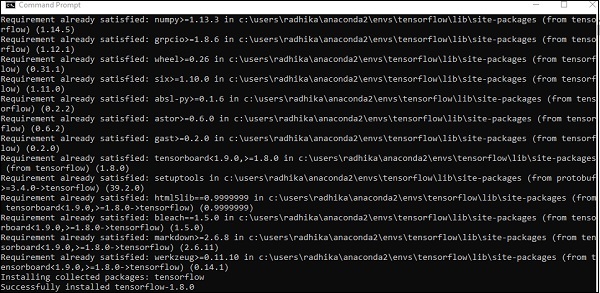
After successful installation, it is important to know the sample program execution of TensorFlow.

Following example helps us understand the basic program creation “Hello World” in TensorFlow.

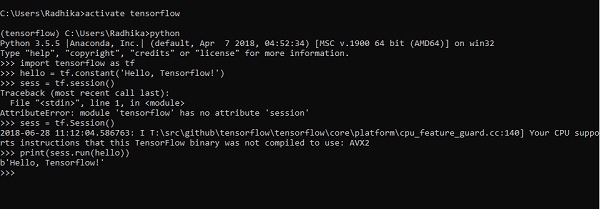
The code for first program implementation is mentioned below −

>> activate tensorflow
>> python (activating python shell)
>> import tensorflow as tf
>> hello = tf.constant(‘Hello, Tensorflow!’)
>> sess = tf.Session()
>> print(sess.run(hello))

Understanding Artificial Intelligence

Artificial Intelligence includes the simulation process of human intelligence by machines and special computer systems. The examples of artificial intelligence include learning, reasoning and self-correction. Applications of AI include speech recognition, expert systems, and image recognition and machine vision.

Machine learning is the branch of artificial intelligence, which deals with systems and algorithms that can learn any new data and data patterns.

Let us focus on the Venn diagram mentioned below for understanding machine learning and deep learning concepts.

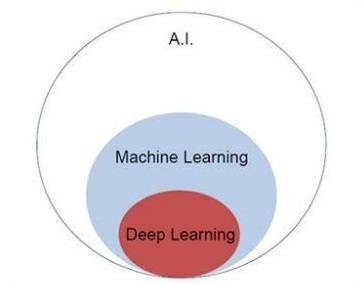
Machine learning includes a section of machine learning and deep learning is a part of machine learning. The ability of program which follows machine learning concepts is to improve its performance of observed data. The main motive of data transformation is to improve its knowledge in order to achieve better results in the future, provide output closer to the desired output for that particular system. Machine learning includes “pattern recognition” which includes the ability to recognize the patterns in data.

The patterns should be trained to show the output in desirable manner.

Machine learning can be trained in two different ways −

Supervised training
Unsupervised training

Supervised Learning

Supervised learning or supervised training includes a procedure where the training set is given as input to the system wherein, each example is labeled with a desired output value. The training in this type is performed using minimization of a particular loss function, which represents the output error with respect to the desired output system.

After completion of training, the accuracy of each model is measured with respect to disjoint examples from training set, also called the validation set.

The best example to illustrate “Supervised learning” is with a bunch of photos given with information included in them. Here, the user can train a model to recognize new photos.

Unsupervised Learning

In unsupervised learning or unsupervised training, include training examples, which are not labeled by the system to which class they belong. The system looks for the data, which share common characteristics, and changes them based on internal knowledge features.This type of learning algorithms are basically used in clustering problems.

The best example to illustrate “Unsupervised learning” is with a bunch of photos with no information included and user trains model with classification and clustering. This type of training algorithm works with assumptions as no information is given.

TensorFlow - Mathematical Foundations

It is important to understand mathematical concepts needed for TensorFlow before creating the basic application in TensorFlow. Mathematics is considered as the heart of any machine learning algorithm. It is with the help of core concepts of Mathematics, a solution for specific machine learning algorithm is defined.

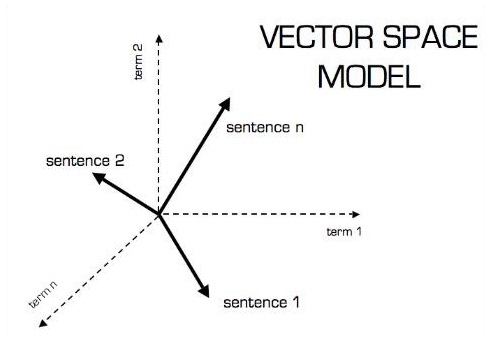
Vector

An array of numbers, which is either continuous or discrete, is defined as a vector. Machine learning algorithms deal with fixed length vectors for better output generation.

Machine learning algorithms deal with multidimensional data so vectors play a crucial role.

The pictorial representation of vector model is as shown below −

Scalar

Scalar can be defined as one-dimensional vector. Scalars are those, which include only magnitude and no direction. With scalars, we are only concerned with the magnitude.

Examples of scalar include weight and height parameters of children.

Matrix

Matrix can be defined as multi-dimensional arrays, which are arranged in the format of rows and columns. The size of matrix is defined by row length and column length. Following figure shows the representation of any specified matrix.

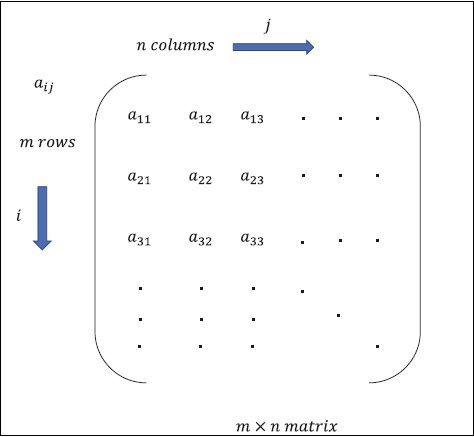
Consider the matrix with “m” rows and “n” columns as mentioned above, the matrix representation will be specified as “m*n matrix” which defined the length of matrix as well.

Mathematical Computations

In this section, we will learn about the different Mathematical Computations in TensorFlow.

Addition of matrices

Addition of two or more matrices is possible if the matrices are of the same dimension. The addition implies addition of each element as per the given position.

Consider the following example to understand how addition of matrices works −

$$Example:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:then\:A+B=\begin{bmatrix}1+5 & 2+6 \\3+7 & 4+8 \end{bmatrix}=\begin{bmatrix}6 & 8 \\10 & 12 \end{bmatrix}$$

Subtraction of matrices

The subtraction of matrices operates in similar fashion like the addition of two matrices. The user can subtract two matrices provided the dimensions are equal.

$$Example:A-\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B-\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}\:then\:A-B-\begin{bmatrix}1-5 & 2-6 \\3-7 & 4-8 \end{bmatrix}-\begin{bmatrix}-4 & -4 \\-4 & -4 \end{bmatrix}$$

Multiplication of matrices

For two matrices A m*n and B p*q to be multipliable, n should be equal to p. The resulting matrix is −

C m*q

$$A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}B=\begin{bmatrix}5 & 6 \\7 & 8 \end{bmatrix}$$

$$c_{11}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=1\times5+2\times7=19\:c_{12}=\begin{bmatrix}1 & 2 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=1\times6+2\times8=22$$

$$c_{21}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}5 \\7 \end{bmatrix}=3\times5+4\times7=43\:c_{22}=\begin{bmatrix}3 & 4 \end{bmatrix}\begin{bmatrix}6 \\8 \end{bmatrix}=3\times6+4\times8=50$$

$$C=\begin{bmatrix}c_{11} & c_{12} \\c_{21} & c_{22} \end{bmatrix}=\begin{bmatrix}19 & 22 \\43 & 50 \end{bmatrix}$$

Transpose of matrix

The transpose of a matrix A, m*n is generally represented by AT (transpose) n*m and is obtained by transposing the column vectors as row vectors.

$$Example:A=\begin{bmatrix}1 & 2 \\3 & 4 \end{bmatrix}\:then\:A^{T}\begin{bmatrix}1 & 3 \\2 & 4 \end{bmatrix}$$

Dot product of vectors

Any vector of dimension n can be represented as a matrix v = R^n*1.

$$v_{1}=\begin{bmatrix}v_{11} \\v_{12} \\\cdot\\\cdot\\\cdot\\v_{1n}\end{bmatrix}v_{2}=\begin{bmatrix}v_{21} \\v_{22} \\\cdot\\\cdot\\\cdot\\v_{2n}\end{bmatrix}$$

The dot product of two vectors is the sum of the product of corresponding components − Components along the same dimension and can be expressed as

$$v_{1}\cdot v_{2}=v_1^Tv_{2}=v_2^Tv_{1}=v_{11}v_{21}+v_{12}v_{22}+\cdot\cdot+v_{1n}v_{2n}=\displaystyle\sum\limits_{k=1}^n v_{1k}v_{2k}$$

The example of dot product of vectors is mentioned below −

$$Example:v_{1}=\begin{bmatrix}1 \\2 \\3\end{bmatrix}v_{2}=\begin{bmatrix}3 \\5 \\-1\end{bmatrix}v_{1}\cdot v_{2}=v_1^Tv_{2}=1\times3+2\times5-3\times1=10$$

Machine Learning and Deep Learning

Artificial Intelligence is one of the most popular trends of recent times. Machine learning and deep learning constitute artificial intelligence. The Venn diagram shown below explains the relationship of machine learning and deep learning −

Machine Learning

Machine learning is the art of science of getting computers to act as per the algorithms designed and programmed. Many researchers think machine learning is the best way to make progress towards human-level AI. Machine learning includes the following types of patterns

Supervised learning pattern
Unsupervised learning pattern

Deep Learning

Deep learning is a subfield of machine learning where concerned algorithms are inspired by the structure and function of the brain called artificial neural networks.

All the value today of deep learning is through supervised learning or learning from labelled data and algorithms.

Each algorithm in deep learning goes through the same process. It includes a hierarchy of nonlinear transformation of input that can be used to generate a statistical model as output.

Consider the following steps that define the Machine Learning process

Identifies relevant data sets and prepares them for analysis.
Chooses the type of algorithm to use
Builds an analytical model based on the algorithm used.
Trains the model on test data sets, revising it as needed.
Runs the model to generate test scores.

Difference between Machine Learning and Deep learning

In this section, we will learn about the difference between Machine Learning and Deep Learning.

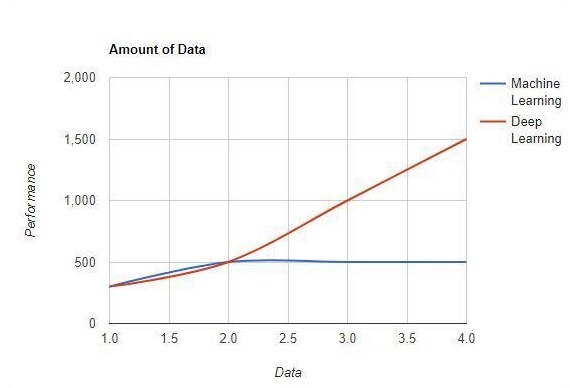
Amount of data

Machine learning works with large amounts of data. It is useful for small amounts of data too. Deep learning on the other hand works efficiently if the amount of data increases rapidly. The following diagram shows the working of machine learning and deep learning with the amount of data −

Hardware Dependencies

Deep learning algorithms are designed to heavily depend on high-end machines unlike the traditional machine learning algorithms. Deep learning algorithms perform a number of matrix multiplication operations, which require a large amount of hardware support.

Feature Engineering

Feature engineering is the process of putting domain knowledge into specified features to reduce the complexity of data and make patterns that are visible to learning algorithms it works.

Example − Traditional machine learning patterns focus on pixels and other attributes needed for feature engineering process. Deep learning algorithms focus on high-level features from data. It reduces the task of developing new feature extractor of every new problem.

Problem Solving Approach

The traditional machine learning algorithms follow a standard procedure to solve the problem. It breaks the problem into parts, solve each one of them and combine them to get the required result. Deep learning focusses in solving the problem from end to end instead of breaking them into divisions.

Execution Time

Execution time is the amount of time required to train an algorithm. Deep learning requires a lot of time to train as it includes a lot of parameters which takes a longer time than usual. Machine learning algorithm comparatively requires less execution time.

Interpretability

Interpretability is the major factor for comparison of machine learning and deep learning algorithms. The main reason is that deep learning is still given a second thought before its usage in industry.

Applications of Machine Learning and Deep Learning

In this section, we will learn about the different applications of Machine Learning and Deep Learning.

Computer vision which is used for facial recognition and attendance mark through fingerprints or vehicle identification through number plate.
Information Retrieval from search engines like text search for image search.
Automated email marketing with specified target identification.
Medical diagnosis of cancer tumors or anomaly identification of any chronic disease.
Natural language processing for applications like photo tagging. The best example to explain this scenario is used in Facebook.
Online Advertising.

Future Trends

With the increasing trend of using data science and machine learning in the industry, it will become important for each organization to inculcate machine learning in their businesses.
Deep learning is gaining more importance than machine learning. Deep learning is proving to be one of the best techniques in state-of-art performance.
Machine learning and deep learning will prove beneficial in research and academics field.

Conclusion

In this article, we had an overview of machine learning and deep learning with illustrations and differences also focusing on future trends. Many of AI applications utilize machine learning algorithms primarily to drive self-service, increase agent productivity and workflows more reliable. Machine learning and deep learning algorithms include an exciting prospect for many businesses and industry leaders.

TensorFlow - Basics

In this chapter, we will learn about the basics of TensorFlow. We will begin by understanding the data structure of tensor.

Tensor Data Structure

Tensors are used as the basic data structures in TensorFlow language. Tensors represent the connecting edges in any flow diagram called the Data Flow Graph. Tensors are defined as multidimensional array or list.

Tensors are identified by the following three parameters −

Rank

Unit of dimensionality described within tensor is called rank. It identifies the number of dimensions of the tensor. A rank of a tensor can be described as the order or n-dimensions of a tensor defined.

Shape

The number of rows and columns together define the shape of Tensor.

Type

Type describes the data type assigned to Tensor’s elements.

A user needs to consider the following activities for building a Tensor −

Build an n-dimensional array
Convert the n-dimensional array.

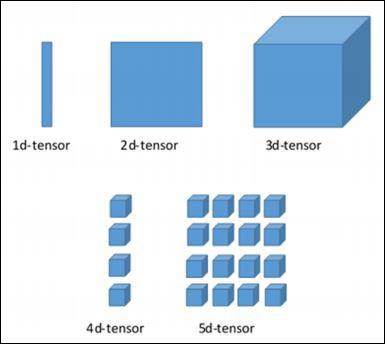
Various Dimensions of TensorFlow

TensorFlow includes various dimensions. The dimensions are described in brief below −

One dimensional Tensor

One dimensional tensor is a normal array structure which includes one set of values of the same data type.

Declaration

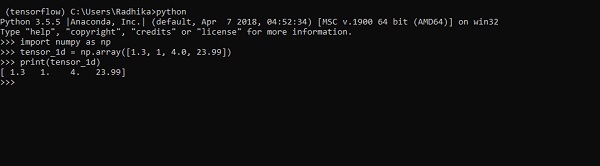
>>> import numpy as np
>>> tensor_1d = np.array([1.3, 1, 4.0, 23.99])
>>> print tensor_1d

The implementation with the output is shown in the screenshot below −

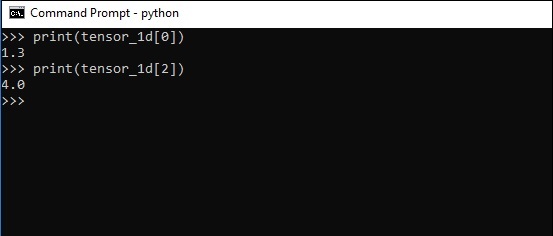
The indexing of elements is same as Python lists. The first element starts with index of 0; to print the values through index, all you need to do is mention the index number.

>>> print tensor_1d[0]
1.3
>>> print tensor_1d[2]
4.0

Two dimensional Tensors

Sequence of arrays are used for creating “two dimensional tensors”.

The creation of two-dimensional tensors is described below −

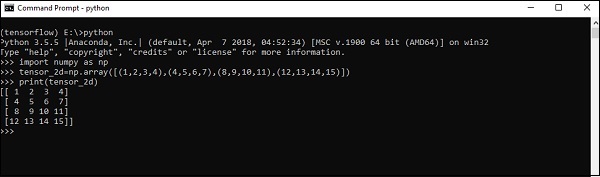
Following is the complete syntax for creating two dimensional arrays −

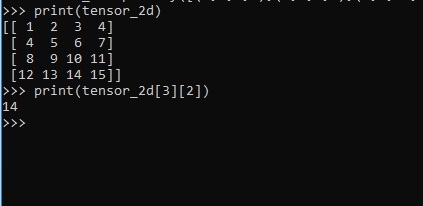
>>> import numpy as np
>>> tensor_2d = np.array([(1,2,3,4),(4,5,6,7),(8,9,10,11),(12,13,14,15)])
>>> print(tensor_2d)
[[ 1 2 3 4]
[ 4 5 6 7]
[ 8 9 10 11]
[12 13 14 15]]
>>>

The specific elements of two dimensional tensors can be tracked with the help of row number and column number specified as index numbers.

>>> tensor_2d[3][2]
14

Tensor Handling and Manipulations

In this section, we will learn about Tensor Handling and Manipulations.

To begin with, let us consider the following code −

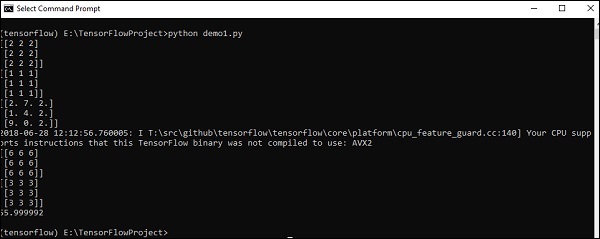
import tensorflow as tf
import numpy as np

matrix1 = np.array([(2,2,2),(2,2,2),(2,2,2)],dtype = 'int32')
matrix2 = np.array([(1,1,1),(1,1,1),(1,1,1)],dtype = 'int32')

print (matrix1)
print (matrix2)

matrix1 = tf.constant(matrix1)
matrix2 = tf.constant(matrix2)
matrix_product = tf.matmul(matrix1, matrix2)
matrix_sum = tf.add(matrix1,matrix2)
matrix_3 = np.array([(2,7,2),(1,4,2),(9,0,2)],dtype = 'float32')
print (matrix_3)

matrix_det = tf.matrix_determinant(matrix_3)
with tf.Session() as sess:
   result1 = sess.run(matrix_product)
   result2 = sess.run(matrix_sum)
   result3 = sess.run(matrix_det)

print (result1)
print (result2)
print (result3)

Output

The above code will generate the following output −

Explanation

We have created multidimensional arrays in the above source code. Now, it is important to understand that we created graph and sessions, which manage the Tensors and generate the appropriate output. With the help of graph, we have the output specifying the mathematical calculations between Tensors.

TensorFlow - Convolutional Neural Networks

After understanding machine-learning concepts, we can now shift our focus to deep learning concepts. Deep learning is a division of machine learning and is considered as a crucial step taken by researchers in recent decades. The examples of deep learning implementation include applications like image recognition and speech recognition.

Following are the two important types of deep neural networks −

Convolutional Neural Networks
Recurrent Neural Networks

In this chapter, we will focus on the CNN, Convolutional Neural Networks.

Convolutional Neural Networks

Convolutional Neural networks are designed to process data through multiple layers of arrays. This type of neural networks is used in applications like image recognition or face recognition. The primary difference between CNN and any other ordinary neural network is that CNN takes input as a two-dimensional array and operates directly on the images rather than focusing on feature extraction which other neural networks focus on.

The dominant approach of CNN includes solutions for problems of recognition. Top companies like Google and Facebook have invested in research and development towards recognition projects to get activities done with greater speed.

A convolutional neural network uses three basic ideas −

Local respective fields
Convolution
Pooling

Let us understand these ideas in detail.

CNN utilizes spatial correlations that exist within the input data. Each concurrent layer of a neural network connects some input neurons. This specific region is called local receptive field. Local receptive field focusses on the hidden neurons. The hidden neurons process the input data inside the mentioned field not realizing the changes outside the specific boundary.

Following is a diagram representation of generating local respective fields −

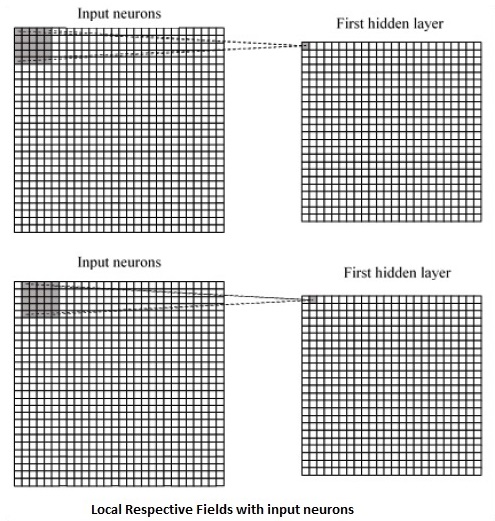
If we observe the above representation, each connection learns a weight of the hidden neuron with an associated connection with movement from one layer to another. Here, individual neurons perform a shift from time to time. This process is called “convolution”.

The mapping of connections from the input layer to the hidden feature map is defined as “shared weights” and bias included is called “shared bias”.

CNN or convolutional neural networks use pooling layers, which are the layers, positioned immediately after CNN declaration. It takes the input from the user as a feature map that comes out of convolutional networks and prepares a condensed feature map. Pooling layers helps in creating layers with neurons of previous layers.

TensorFlow Implementation of CNN

In this section, we will learn about the TensorFlow implementation of CNN. The steps,which require the execution and proper dimension of the entire network, are as shown below −

Step 1 − Include the necessary modules for TensorFlow and the data set modules, which are needed to compute the CNN model.

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data

Step 2 − Declare a function called run_cnn(), which includes various parameters and optimization variables with declaration of data placeholders. These optimization variables will declare the training pattern.

def run_cnn():
   mnist = input_data.read_data_sets("MNIST_data/", one_hot = True)
   learning_rate = 0.0001
   epochs = 10
   batch_size = 50

Step 3 − In this step, we will declare the training data placeholders with input parameters - for 28 x 28 pixels = 784. This is the flattened image data that is drawn from mnist.train.nextbatch().

We can reshape the tensor according to our requirements. The first value (-1) tells function to dynamically shape that dimension based on the amount of data passed to it. The two middle dimensions are set to the image size (i.e. 28 x 28).

x = tf.placeholder(tf.float32, [None, 784])
x_shaped = tf.reshape(x, [-1, 28, 28, 1])
y = tf.placeholder(tf.float32, [None, 10])

Step 4 − Now it is important to create some convolutional layers −

layer1 = create_new_conv_layer(x_shaped, 1, 32, [5, 5], [2, 2], name = 'layer1')
layer2 = create_new_conv_layer(layer1, 32, 64, [5, 5], [2, 2], name = 'layer2')

Step 5 − Let us flatten the output ready for the fully connected output stage - after two layers of stride 2 pooling with the dimensions of 28 x 28, to dimension of 14 x 14 or minimum 7 x 7 x,y co-ordinates, but with 64 output channels. To create the fully connected with "dense" layer, the new shape needs to be [-1, 7 x 7 x 64]. We can set up some weights and bias values for this layer, then activate with ReLU.

flattened = tf.reshape(layer2, [-1, 7 * 7 * 64])

wd1 = tf.Variable(tf.truncated_normal([7 * 7 * 64, 1000], stddev = 0.03), name = 'wd1')
bd1 = tf.Variable(tf.truncated_normal([1000], stddev = 0.01), name = 'bd1')

dense_layer1 = tf.matmul(flattened, wd1) + bd1
dense_layer1 = tf.nn.relu(dense_layer1)

Step 6 − Another layer with specific softmax activations with the required optimizer defines the accuracy assessment, which makes the setup of initialization operator.

wd2 = tf.Variable(tf.truncated_normal([1000, 10], stddev = 0.03), name = 'wd2')
bd2 = tf.Variable(tf.truncated_normal([10], stddev = 0.01), name = 'bd2')

dense_layer2 = tf.matmul(dense_layer1, wd2) + bd2
y_ = tf.nn.softmax(dense_layer2)

cross_entropy = tf.reduce_mean(
   tf.nn.softmax_cross_entropy_with_logits(logits = dense_layer2, labels = y))

optimiser = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cross_entropy)

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

init_op = tf.global_variables_initializer()

Step 7 − We should set up recording variables. This adds up a summary to store the accuracy of data.

tf.summary.scalar('accuracy', accuracy)
   merged = tf.summary.merge_all()
   writer = tf.summary.FileWriter('E:\TensorFlowProject')
   
   with tf.Session() as sess:
      sess.run(init_op)
      total_batch = int(len(mnist.train.labels) / batch_size)
      
      for epoch in range(epochs):
         avg_cost = 0
      for i in range(total_batch):
         batch_x, batch_y = mnist.train.next_batch(batch_size = batch_size)
            _, c = sess.run([optimiser, cross_entropy], feed_dict = {
            x:batch_x, y: batch_y})
            avg_cost += c / total_batch
         test_acc = sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
            mnist.test.labels})
            summary = sess.run(merged, feed_dict = {x: mnist.test.images, y:
            mnist.test.labels})
         writer.add_summary(summary, epoch)

   print("\nTraining complete!")
   writer.add_graph(sess.graph)
   print(sess.run(accuracy, feed_dict = {x: mnist.test.images, y:
      mnist.test.labels}))

def create_new_conv_layer(
   input_data, num_input_channels, num_filters,filter_shape, pool_shape, name):

   conv_filt_shape = [
      filter_shape[0], filter_shape[1], num_input_channels, num_filters]

   weights = tf.Variable(
      tf.truncated_normal(conv_filt_shape, stddev = 0.03), name = name+'_W')
   bias = tf.Variable(tf.truncated_normal([num_filters]), name = name+'_b')

#Out layer defines the output
   out_layer =
      tf.nn.conv2d(input_data, weights, [1, 1, 1, 1], padding = 'SAME')

   out_layer += bias
   out_layer = tf.nn.relu(out_layer)
   ksize = [1, pool_shape[0], pool_shape[1], 1]
   strides = [1, 2, 2, 1]
   out_layer = tf.nn.max_pool(
      out_layer, ksize = ksize, strides = strides, padding = 'SAME')

   return out_layer

if __name__ == "__main__":
run_cnn()

Following is the output generated by the above code −

See @{tf.nn.softmax_cross_entropy_with_logits_v2}.

2018-09-19 17:22:58.802268: I
T:\src\github\tensorflow\tensorflow\core\platform\cpu_feature_guard.cc:140]
Your CPU supports instructions that this TensorFlow binary was not compiled to
use: AVX2

2018-09-19 17:25:41.522845: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.

2018-09-19 17:25:44.630941: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 501760000 exceeds 10% of system memory.

Epoch: 1 cost = 0.676 test accuracy: 0.940

2018-09-19 17:26:51.987554: W
T:\src\github\tensorflow\tensorflow\core\framework\allocator.cc:101] Allocation
of 1003520000 exceeds 10% of system memory.

TensorFlow - Recurrent Neural Networks

Recurrent neural networks is a type of deep learning-oriented algorithm, which follows a sequential approach. In neural networks, we always assume that each input and output is independent of all other layers. These type of neural networks are called recurrent because they perform mathematical computations in sequential manner.

Consider the following steps to train a recurrent neural network −

Step 1 − Input a specific example from dataset.

Step 2 − Network will take an example and compute some calculations using randomly initialized variables.

Step 3 − A predicted result is then computed.

Step 4 − The comparison of actual result generated with the expected value will produce an error.

Step 5 − To trace the error, it is propagated through same path where the variables are also adjusted.

Step 6 − The steps from 1 to 5 are repeated until we are confident that the variables declared to get the output are defined properly.

Step 7 − A systematic prediction is made by applying these variables to get new unseen input.

The schematic approach of representing recurrent neural networks is described below −

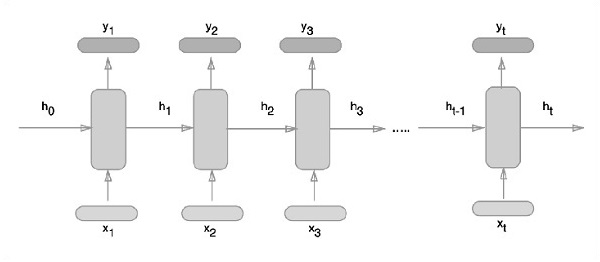
Recurrent Neural Network Implementation with TensorFlow

In this section, we will learn how to implement recurrent neural network with TensorFlow.

Step 1 − TensorFlow includes various libraries for specific implementation of the recurrent neural network module.

#Import necessary modules
from __future__ import print_function

import tensorflow as tf
from tensorflow.contrib import rnn
from tensorflow.examples.tutorials.mnist import input_data
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True)

As mentioned above, the libraries help in defining the input data, which forms the primary part of recurrent neural network implementation.

Step 2 − Our primary motive is to classify the images using a recurrent neural network, where we consider every image row as a sequence of pixels. MNIST image shape is specifically defined as 28*28 px. Now we will handle 28 sequences of 28 steps for each sample that is mentioned. We will define the input parameters to get the sequential pattern done.

n_input = 28 # MNIST data input with img shape 28*28
n_steps = 28
n_hidden = 128
n_classes = 10

# tf Graph input
x = tf.placeholder("float", [None, n_steps, n_input])
y = tf.placeholder("float", [None, n_classes]
weights = {
   'out': tf.Variable(tf.random_normal([n_hidden, n_classes]))
}
biases = {
   'out': tf.Variable(tf.random_normal([n_classes]))
}

Step 3 − Compute the results using a defined function in RNN to get the best results. Here, each data shape is compared with current input shape and the results are computed to maintain the accuracy rate.

def RNN(x, weights, biases):
   x = tf.unstack(x, n_steps, 1)

   # Define a lstm cell with tensorflow
   lstm_cell = rnn.BasicLSTMCell(n_hidden, forget_bias=1.0)

   # Get lstm cell output
   outputs, states = rnn.static_rnn(lstm_cell, x, dtype = tf.float32)

   # Linear activation, using rnn inner loop last output
   return tf.matmul(outputs[-1], weights['out']) + biases['out']

pred = RNN(x, weights, biases)

# Define loss and optimizer
cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits = pred, labels = y))
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost)

# Evaluate model
correct_pred = tf.equal(tf.argmax(pred,1), tf.argmax(y,1))
accuracy = tf.reduce_mean(tf.cast(correct_pred, tf.float32))

# Initializing the variables
init = tf.global_variables_initializer()

Step 4 − In this step, we will launch the graph to get the computational results. This also helps in calculating the accuracy for test results.

with tf.Session() as sess:
   sess.run(init)
   step = 1
   # Keep training until reach max iterations
   
   while step * batch_size < training_iters:
      batch_x, batch_y = mnist.train.next_batch(batch_size)
      batch_x = batch_x.reshape((batch_size, n_steps, n_input))
      sess.run(optimizer, feed_dict={x: batch_x, y: batch_y})
      
      if step % display_step == 0:
         # Calculate batch accuracy
         acc = sess.run(accuracy, feed_dict={x: batch_x, y: batch_y})
         
         # Calculate batch loss
         loss = sess.run(cost, feed_dict={x: batch_x, y: batch_y})
         
         print("Iter " + str(step*batch_size) + ", Minibatch Loss= " + \
            "{:.6f}".format(loss) + ", Training Accuracy= " + \
            "{:.5f}".format(acc))
      step += 1
   print("Optimization Finished!")
      test_len = 128
   test_data = mnist.test.images[:test_len].reshape((-1, n_steps, n_input))
   
   test_label = mnist.test.labels[:test_len]
   print("Testing Accuracy:", \
      sess.run(accuracy, feed_dict={x: test_data, y: test_label}))

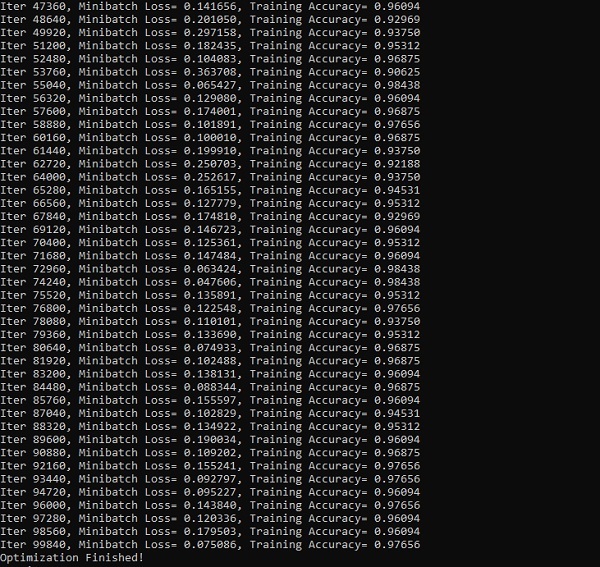
The screenshots below show the output generated −

Recurrent Neural Networks Implementation Output

Recurrent Neural Networks Implementation Output TransFlow

TensorFlow - TensorBoard Visualization

TensorFlow includes a visualization tool, which is called the TensorBoard. It is used for analyzing Data Flow Graph and also used to understand machine-learning models. The important feature of TensorBoard includes a view of different types of statistics about the parameters and details of any graph in vertical alignment.

Deep neural network includes up to 36,000 nodes. TensorBoard helps in collapsing these nodes in high-level blocks and highlighting the identical structures. This allows better analysis of graph focusing on the primary sections of the computation graph. The TensorBoard visualization is said to be very interactive where a user can pan, zoom and expand the nodes to display the details.

The following schematic diagram representation shows the complete working of TensorBoard visualization −

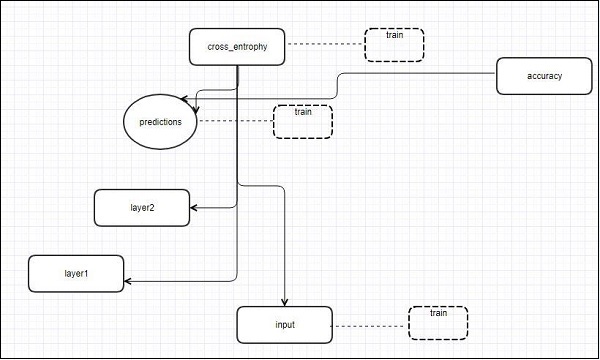
The algorithms collapse nodes into high-level blocks and highlight the specific groups with identical structures, which separate high-degree nodes. The TensorBoard thus created is useful and is treated equally important for tuning a machine learning model. This visualization tool is designed for the configuration log file with summary information and details that need to be displayed.

Let us focus on the demo example of TensorBoard visualization with the help of the following code −

import tensorflow as tf 

# Constants creation for TensorBoard visualization 
a = tf.constant(10,name = "a") 
b = tf.constant(90,name = "b") 
y = tf.Variable(a+b*2,name = 'y') 
model = tf.initialize_all_variables() #Creation of model 

with tf.Session() as session: 
   merged = tf.merge_all_summaries() 
   writer = tf.train.SummaryWriter("/tmp/tensorflowlogs",session.graph) 
   session.run(model) 
   print(session.run(y))

The following table shows the various symbols of TensorBoard visualization used for the node representation −

TensorFlow - Word Embedding

Word embedding is the concept of mapping from discrete objects such as words to vectors and real numbers. It is important for input for machine learning. The concept includes standard functions, which effectively transform discrete input objects to useful vectors.

The sample illustration of input of word embedding is as shown below −

blue: (0.01359, 0.00075997, 0.24608, ..., -0.2524, 1.0048, 0.06259)
blues: (0.01396, 0.11887, -0.48963, ..., 0.033483, -0.10007, 0.1158)
orange: (-0.24776, -0.12359, 0.20986, ..., 0.079717, 0.23865, -0.014213)
oranges: (-0.35609, 0.21854, 0.080944, ..., -0.35413, 0.38511, -0.070976)

Word2vec

Word2vec is the most common approach used for unsupervised word embedding technique. It trains the model in such a way that a given input word predicts the word’s context by using skip-grams.

TensorFlow enables many ways to implement this kind of model with increasing levels of sophistication and optimization and using multithreading concepts and higher-level abstractions.

import os 
import math 
import numpy as np 
import tensorflow as tf 

from tensorflow.contrib.tensorboard.plugins import projector 
batch_size = 64 
embedding_dimension = 5 
negative_samples = 8 
LOG_DIR = "logs/word2vec_intro" 

digit_to_word_map = {
   1: "One", 
   2: "Two", 
   3: "Three", 
   4: "Four", 
   5: "Five", 
   6: "Six", 
   7: "Seven", 
   8: "Eight", 
   9: "Nine"} 
sentences = [] 

# Create two kinds of sentences - sequences of odd and even digits. 
   for i in range(10000): 
   rand_odd_ints = np.random.choice(range(1, 10, 2), 3) 
      sentences.append(" ".join([digit_to_word_map[r] for r in rand_odd_ints])) 
   rand_even_ints = np.random.choice(range(2, 10, 2), 3) 
      sentences.append(" ".join([digit_to_word_map[r] for r in rand_even_ints])) 
   
# Map words to indices
word2index_map = {} 
index = 0 

for sent in sentences: 
   for word in sent.lower().split(): 
   
   if word not in word2index_map: 
      word2index_map[word] = index 
      index += 1 
index2word_map = {index: word for word, index in word2index_map.items()} 

vocabulary_size = len(index2word_map) 

# Generate skip-gram pairs 
skip_gram_pairs = [] 

for sent in sentences: 
   tokenized_sent = sent.lower().split() 
   
   for i in range(1, len(tokenized_sent)-1):        
      word_context_pair = [[word2index_map[tokenized_sent[i-1]], 
         word2index_map[tokenized_sent[i+1]]], word2index_map[tokenized_sent[i]]] 
      
      skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][0]]) 
      skip_gram_pairs.append([word_context_pair[1], word_context_pair[0][1]]) 

def get_skipgram_batch(batch_size): 
   instance_indices = list(range(len(skip_gram_pairs))) 
      np.random.shuffle(instance_indices)
   batch = instance_indices[:batch_size] 
   x = [skip_gram_pairs[i][0] for i in batch] 
   y = [[skip_gram_pairs[i][1]] for i in batch] 
   return x, y 
   
# batch example 
x_batch, y_batch = get_skipgram_batch(8) 
x_batch 
y_batch 
[index2word_map[word] for word in x_batch] [index2word_map[word[0]] for word in y_batch] 

# Input data, labels train_inputs = tf.placeholder(tf.int32, shape = [batch_size]) 
   train_labels = tf.placeholder(tf.int32, shape = [batch_size, 1]) 

# Embedding lookup table currently only implemented in CPU with 
   tf.name_scope("embeddings"): 
   embeddings = tf.Variable(    
      tf.random_uniform([vocabulary_size, embedding_dimension], -1.0, 1.0), 
         name = 'embedding') 
   # This is essentialy a lookup table 
   embed = tf.nn.embedding_lookup(embeddings, train_inputs) 
   
# Create variables for the NCE loss
nce_weights = tf.Variable(     
   tf.truncated_normal([vocabulary_size, embedding_dimension], stddev = 1.0 / 
      math.sqrt(embedding_dimension))) 
   
nce_biases = tf.Variable(tf.zeros([vocabulary_size])) 

loss = tf.reduce_mean(     
   tf.nn.nce_loss(weights = nce_weights, biases = nce_biases, inputs = embed, 
   labels = train_labels,num_sampled = negative_samples, 
   num_classes = vocabulary_size)) tf.summary.scalar("NCE_loss", loss) 
   
# Learning rate decay 
global_step = tf.Variable(0, trainable = False) 
   learningRate = tf.train.exponential_decay(learning_rate = 0.1, 
   global_step = global_step, decay_steps = 1000, decay_rate = 0.95, staircase = True) 

train_step = tf.train.GradientDescentOptimizer(learningRate).minimize(loss) 
   merged = tf.summary.merge_all() 
with tf.Session() as sess: 
   train_writer = tf.summary.FileWriter(LOG_DIR,    
      graph = tf.get_default_graph()) 
   saver = tf.train.Saver() 
   
   with open(os.path.join(LOG_DIR, 'metadata.tsv'), "w") as metadata: 
      metadata.write('Name\tClass\n') for k, v in index2word_map.items(): 
      metadata.write('%s\t%d\n' % (v, k)) 
   
   config = projector.ProjectorConfig() 
   embedding = config.embeddings.add() embedding.tensor_name = embeddings.name 
   
   # Link this tensor to its metadata file (e.g. labels). 
   embedding.metadata_path = os.path.join(LOG_DIR, 'metadata.tsv') 
      projector.visualize_embeddings(train_writer, config) 
   
   tf.global_variables_initializer().run() 
   
   for step in range(1000): 
      x_batch, y_batch = get_skipgram_batch(batch_size) summary, _ = sess.run(
         [merged, train_step], feed_dict = {train_inputs: x_batch, train_labels: y_batch})
      train_writer.add_summary(summary, step)
      
      if step % 100 == 0:
         saver.save(sess, os.path.join(LOG_DIR, "w2v_model.ckpt"), step)
         loss_value = sess.run(loss, feed_dict = {
            train_inputs: x_batch, train_labels: y_batch})
         print("Loss at %d: %.5f" % (step, loss_value))

   # Normalize embeddings before using
   norm = tf.sqrt(tf.reduce_sum(tf.square(embeddings), 1, keep_dims = True))
   normalized_embeddings = embeddings /
      norm normalized_embeddings_matrix = sess.run(normalized_embeddings)
   
ref_word = normalized_embeddings_matrix[word2index_map["one"]]

cosine_dists = np.dot(normalized_embeddings_matrix, ref_word)
ff = np.argsort(cosine_dists)[::-1][1:10] for f in ff: print(index2word_map[f])
print(cosine_dists[f])

Output

The above code generates the following output −

TensorFlow - Single Layer Perceptron

For understanding single layer perceptron, it is important to understand Artificial Neural Networks (ANN). Artificial neural networks is the information processing system the mechanism of which is inspired with the functionality of biological neural circuits. An artificial neural network possesses many processing units connected to each other. Following is the schematic representation of artificial neural network −

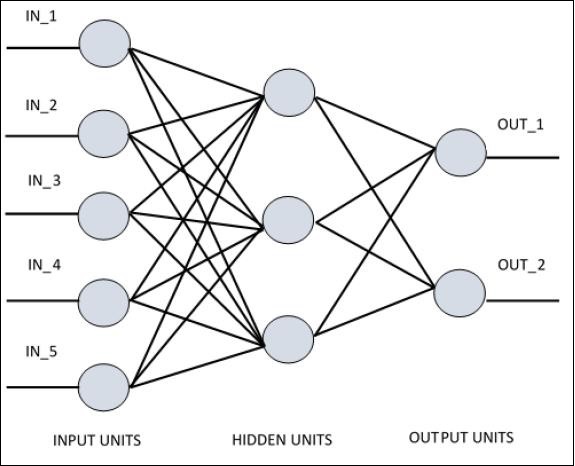
The diagram shows that the hidden units communicate with the external layer. While the input and output units communicate only through the hidden layer of the network.

The pattern of connection with nodes, the total number of layers and level of nodes between inputs and outputs with the number of neurons per layer define the architecture of a neural network.

There are two types of architecture. These types focus on the functionality artificial neural networks as follows −

Single Layer Perceptron
Multi-Layer Perceptron

Single Layer Perceptron

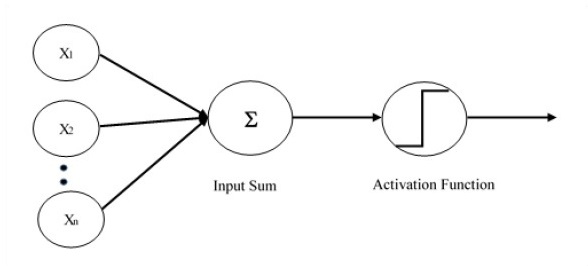
Single layer perceptron is the first proposed neural model created. The content of the local memory of the neuron consists of a vector of weights. The computation of a single layer perceptron is performed over the calculation of sum of the input vector each with the value multiplied by corresponding element of vector of the weights. The value which is displayed in the output will be the input of an activation function.

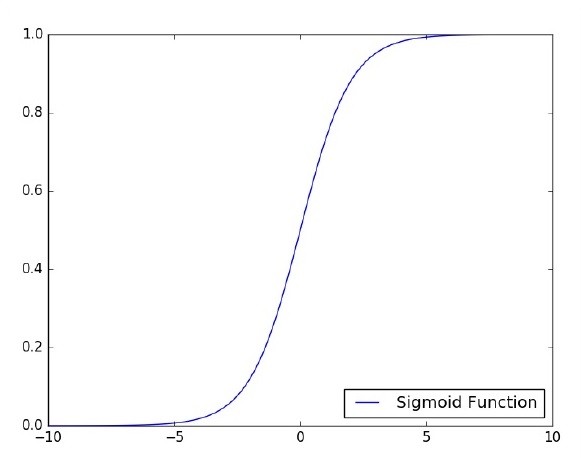
Let us focus on the implementation of single layer perceptron for an image classification problem using TensorFlow. The best example to illustrate the single layer perceptron is through representation of “Logistic Regression”.

Now, let us consider the following basic steps of training logistic regression −

The weights are initialized with random values at the beginning of the training.
For each element of the training set, the error is calculated with the difference between desired output and the actual output. The error calculated is used to adjust the weights.
The process is repeated until the error made on the entire training set is not less than the specified threshold, until the maximum number of iterations is reached.

The complete code for evaluation of logistic regression is mentioned below −

# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.01 
training_epochs = 25 
batch_size = 100 
display_step = 1 

# tf Graph Input 
x = tf.placeholder("float", [None, 784]) # mnist data image of shape 28*28 = 784 
y = tf.placeholder("float", [None, 10]) # 0-9 digits recognition => 10 classes 

# Create model 
# Set model weights 
W = tf.Variable(tf.zeros([784, 10])) 
b = tf.Variable(tf.zeros([10])) 

# Construct model 
activation = tf.nn.softmax(tf.matmul(x, W) + b) # Softmax 

# Minimize error using cross entropy 
cross_entropy = y*tf.log(activation) 
cost = tf.reduce_mean\ (-tf.reduce_sum\ (cross_entropy,reduction_indices = 1)) 

optimizer = tf.train.\ GradientDescentOptimizer(learning_rate).minimize(cost) 

#Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables init = tf.initialize_all_variables()
# Launch the graph 
with tf.Session() as sess:
   sess.run(init)
   
   # Training cycle
   for epoch in range(training_epochs):
      avg_cost = 0.
      total_batch = int(mnist.train.num_examples/batch_size)
      
      # Loop over all batches
      for i in range(total_batch):
         batch_xs, batch_ys = \ mnist.train.next_batch(batch_size)
         # Fit training using batch data sess.run(optimizer, \ feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss avg_cost += sess.run(cost, \ feed_dict = {
            x: batch_xs, \ y: batch_ys})/total_batch
      # Display logs per epoch step
      if epoch % display_step == 0:
         print ("Epoch:", '%04d' % (epoch+1), "cost=", "{:.9f}".format(avg_cost))
            avg_set.append(avg_cost) epoch_set.append(epoch+1)
   print ("Training phase finished")
    
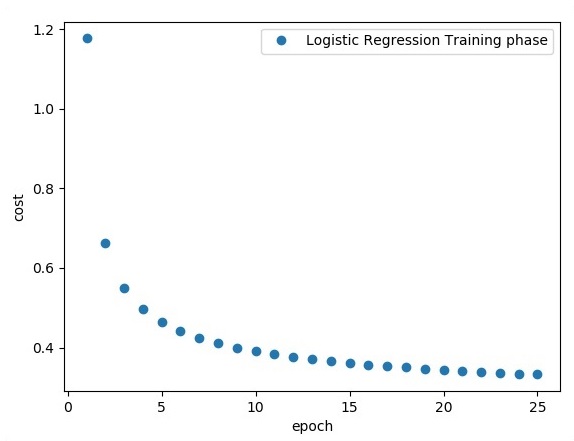
   plt.plot(epoch_set,avg_set, 'o', label = 'Logistic Regression Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
    
   # Test model 
   correct_prediction = tf.equal(tf.argmax(activation, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) print 
      ("Model accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels}))

Output

The above code generates the following output −

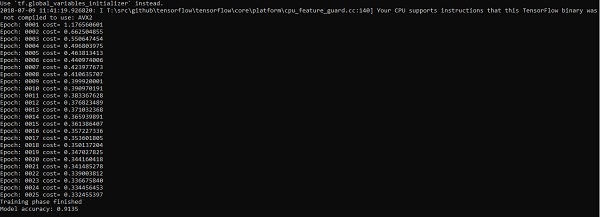
The logistic regression is considered as a predictive analysis. Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal or independent variables.

TensorFlow - Linear Regression

In this chapter, we will focus on the basic example of linear regression implementation using TensorFlow. Logistic regression or linear regression is a supervised machine learning approach for the classification of order discrete categories. Our goal in this chapter is to build a model by which a user can predict the relationship between predictor variables and one or more independent variables.

The relationship between these two variables is cons −idered linear. If y is the dependent variable and x is considered as the independent variable, then the linear regression relationship of two variables will look like the following equation −

Y = Ax+b

We will design an algorithm for linear regression. This will allow us to understand the following two important concepts −

Cost Function
Gradient descent algorithms

The schematic representation of linear regression is mentioned below −

Schematic Representation Linear Regression

The graphical view of the equation of linear regression is mentioned below −

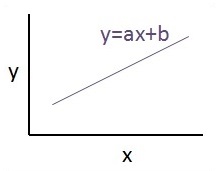
Steps to design an algorithm for linear regression

We will now learn about the steps that help in designing an algorithm for linear regression.

Step 1

It is important to import the necessary modules for plotting the linear regression module. We start importing the Python library NumPy and Matplotlib.

import numpy as np 
import matplotlib.pyplot as plt

Step 2

Define the number of coefficients necessary for logistic regression.

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78

Step 3

Iterate the variables for generating 300 random points around the regression equation −

Y = 0.22x+0.78

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y])

Step 4

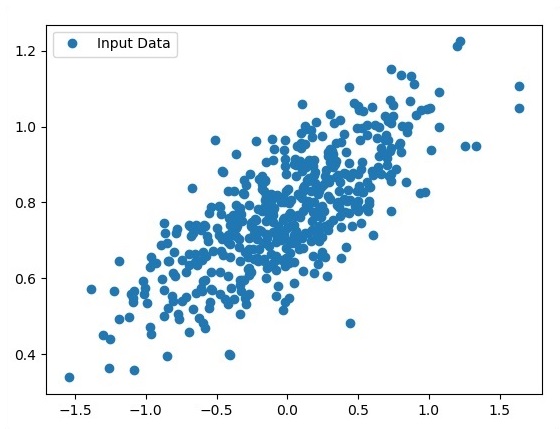
View the generated points using Matplotlib.

fplt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() plt.show()

The complete code for logistic regression is as follows −

import numpy as np 
import matplotlib.pyplot as plt 

number_of_points = 500 
x_point = [] 
y_point = [] 
a = 0.22 
b = 0.78 

for i in range(number_of_points): 
   x = np.random.normal(0.0,0.5) 
   y = a*x + b +np.random.normal(0.0,0.1) x_point.append([x]) 
   y_point.append([y]) 
   
plt.plot(x_point,y_point, 'o', label = 'Input Data') plt.legend() 
plt.show()

The number of points which is taken as input is considered as input data.

TensorFlow - TFLearn And Its Installation

TFLearn can be defined as a modular and transparent deep learning aspect used in TensorFlow framework. The main motive of TFLearn is to provide a higher level API to TensorFlow for facilitating and showing up new experiments.

Consider the following important features of TFLearn −

TFLearn is easy to use and understand.
It includes easy concepts to build highly modular network layers, optimizers and various metrics embedded within them.
It includes full transparency with TensorFlow work system.
It includes powerful helper functions to train the built in tensors which accept multiple inputs, outputs and optimizers.
It includes easy and beautiful graph visualization.
The graph visualization includes various details of weights, gradients and activations.

Install TFLearn by executing the following command −

pip install tflearn

Upon execution of the above code, the following output will be generated −

The following illustration shows the implementation of TFLearn with Random Forest classifier −

from __future__ import division, print_function, absolute_import

#TFLearn module implementation
import tflearn
from tflearn.estimators import RandomForestClassifier

# Data loading and pre-processing with respect to dataset
import tflearn.datasets.mnist as mnist
X, Y, testX, testY = mnist.load_data(one_hot = False)

m = RandomForestClassifier(n_estimators = 100, max_nodes = 1000)
m.fit(X, Y, batch_size = 10000, display_step = 10)

print("Compute the accuracy on train data:")
print(m.evaluate(X, Y, tflearn.accuracy_op))

print("Compute the accuracy on test set:")
print(m.evaluate(testX, testY, tflearn.accuracy_op))

print("Digits for test images id 0 to 5:")
print(m.predict(testX[:5]))

print("True digits:")
print(testY[:5])

TensorFlow - CNN And RNN Difference

In this chapter, we will focus on the difference between CNN and RNN −

CNN	RNN
It is suitable for spatial data such as images.	RNN is suitable for temporal data, also called sequential data.
CNN is considered to be more powerful than RNN.	RNN includes less feature compatibility when compared to CNN.
This network takes fixed size inputs and generates fixed size outputs.	RNN can handle arbitrary input/output lengths.
CNN is a type of feed-forward artificial neural network with variations of multilayer perceptrons designed to use minimal amounts of preprocessing.	RNN unlike feed forward neural networks - can use their internal memory to process arbitrary sequences of inputs.
CNNs use connectivity pattern between the neurons. This is inspired by the organization of the animal visual cortex, whose individual neurons are arranged in such a way that they respond to overlapping regions tiling the visual field.	Recurrent neural networks use time-series information - what a user spoke last will impact what he/she will speak next.
CNNs are ideal for images and video processing.	RNNs are ideal for text and speech analysis.

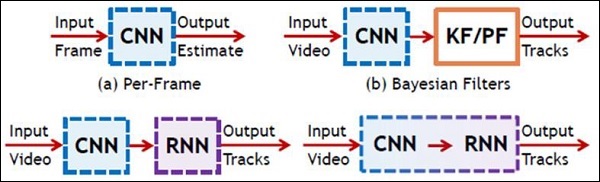
Following illustration shows the schematic representation of CNN and RNN −

TensorFlow - Keras

Keras is compact, easy to learn, high-level Python library run on top of TensorFlow framework. It is made with focus of understanding deep learning techniques, such as creating layers for neural networks maintaining the concepts of shapes and mathematical details. The creation of freamework can be of the following two types −

Sequential API
Functional API

Consider the following eight steps to create deep learning model in Keras −

Loading the data
Preprocess the loaded data
Definition of model
Compiling the model
Fit the specified model
Evaluate it
Make the required predictions
Save the model

We will use the Jupyter Notebook for execution and display of output as shown below −

Step 1 − Loading the data and preprocessing the loaded data is implemented first to execute the deep learning model.

import warnings
warnings.filterwarnings('ignore')

import numpy as np
np.random.seed(123) # for reproducibility

from keras.models import Sequential
from keras.layers import Flatten, MaxPool2D, Conv2D, Dense, Reshape, Dropout
from keras.utils import np_utils
Using TensorFlow backend.
from keras.datasets import mnist

# Load pre-shuffled MNIST data into train and test sets
(X_train, y_train), (X_test, y_test) = mnist.load_data()
X_train = X_train.reshape(X_train.shape[0], 28, 28, 1)
X_test = X_test.reshape(X_test.shape[0], 28, 28, 1)
X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255
Y_train = np_utils.to_categorical(y_train, 10)
Y_test = np_utils.to_categorical(y_test, 10)

This step can be defined as “Import libraries and Modules” which means all the libraries and modules are imported as an initial step.

Step 2 − In this step, we will define the model architecture −

model = Sequential()
model.add(Conv2D(32, 3, 3, activation = 'relu', input_shape = (28,28,1)))
model.add(Conv2D(32, 3, 3, activation = 'relu'))
model.add(MaxPool2D(pool_size = (2,2)))
model.add(Dropout(0.25))
model.add(Flatten())
model.add(Dense(128, activation = 'relu'))
model.add(Dropout(0.5))
model.add(Dense(10, activation = 'softmax'))

Step 3 − Let us now compile the specified model −

model.compile(loss = 'categorical_crossentropy', optimizer = 'adam', metrics = ['accuracy'])

Step 4 − We will now fit the model using training data −

model.fit(X_train, Y_train, batch_size = 32, epochs = 10, verbose = 1)

The output of iterations created is as follows −

Epoch 1/10 60000/60000 [==============================] - 65s - 
loss: 0.2124 - 
acc: 0.9345 
Epoch 2/10 60000/60000 [==============================] - 62s - 
loss: 0.0893 - 
acc: 0.9740 
Epoch 3/10 60000/60000 [==============================] - 58s - 
loss: 0.0665 - 
acc: 0.9802 
Epoch 4/10 60000/60000 [==============================] - 62s - 
loss: 0.0571 - 
acc: 0.9830 
Epoch 5/10 60000/60000 [==============================] - 62s - 
loss: 0.0474 - 
acc: 0.9855 
Epoch 6/10 60000/60000 [==============================] - 59s -
loss: 0.0416 - 
acc: 0.9871 
Epoch 7/10 60000/60000 [==============================] - 61s - 
loss: 0.0380 - 
acc: 0.9877 
Epoch 8/10 60000/60000 [==============================] - 63s - 
loss: 0.0333 - 
acc: 0.9895 
Epoch 9/10 60000/60000 [==============================] - 64s - 
loss: 0.0325 - 
acc: 0.9898 
Epoch 10/10 60000/60000 [==============================] - 60s - 
loss: 0.0284 - 
acc: 0.9910

TensorFlow - Distributed Computing

This chapter will focus on how to get started with distributed TensorFlow. The aim is to help developers understand the basic distributed TF concepts that are reoccurring, such as TF servers. We will use the Jupyter Notebook for evaluating distributed TensorFlow. The implementation of distributed computing with TensorFlow is mentioned below −

Step 1 − Import the necessary modules mandatory for distributed computing −

import tensorflow as tf

Step 2 − Create a TensorFlow cluster with one node. Let this node be responsible for a job that that has name "worker" and that will operate one take at localhost:2222.

cluster_spec = tf.train.ClusterSpec({'worker' : ['localhost:2222']})
server = tf.train.Server(cluster_spec)
server.target

The above scripts generate the following output −

'grpc://localhost:2222'
The server is currently running.

Step 3 − The server configuration with respective session can be calculated by executing the following command −

server.server_def

The above command generates the following output −

cluster {
   job {
      name: "worker"
      tasks {
         value: "localhost:2222"
      }
   }
}
job_name: "worker"
protocol: "grpc"

Step 4 − Launch a TensorFlow session with the execution engine being the server. Use TensorFlow to create a local server and use lsof to find out the location of the server.

sess = tf.Session(target = server.target)
server = tf.train.Server.create_local_server()

Step 5 − View devices available in this session and close the respective session.

devices = sess.list_devices()
for d in devices:
   print(d.name)
sess.close()

The above command generates the following output −

/job:worker/replica:0/task:0/device:CPU:0

TensorFlow - Exporting

Here, we will focus on MetaGraph formation in TensorFlow. This will help us understand export module in TensorFlow. The MetaGraph contains the basic information, which is required to train, perform evaluation, or run inference on a previously trained graph.

Following is the code snippet for the same −

def export_meta_graph(filename = None, collection_list = None, as_text = False): 
   """this code writes `MetaGraphDef` to save_path/filename. 
   
   Arguments: 
   filename: Optional meta_graph filename including the path. collection_list: 
      List of string keys to collect. as_text: If `True`, 
      writes the meta_graph as an ASCII proto. 
   
   Returns: 
   A `MetaGraphDef` proto. """

One of the typical usage model for the same is mentioned below −

# Build the model ... 
with tf.Session() as sess: 
   # Use the model ... 
# Export the model to /tmp/my-model.meta. 
meta_graph_def = tf.train.export_meta_graph(filename = '/tmp/my-model.meta')

TensorFlow - Multi-Layer Perceptron Learning

Multi-Layer perceptron defines the most complicated architecture of artificial neural networks. It is substantially formed from multiple layers of perceptron.

The diagrammatic representation of multi-layer perceptron learning is as shown below −

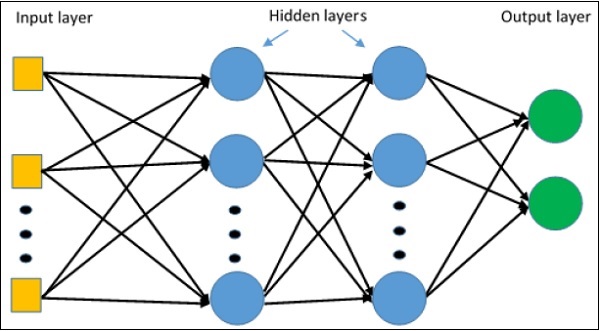
MLP networks are usually used for supervised learning format. A typical learning algorithm for MLP networks is also called back propagation’s algorithm.

Now, we will focus on the implementation with MLP for an image classification problem.

# Import MINST data 
from tensorflow.examples.tutorials.mnist import input_data 
mnist = input_data.read_data_sets("/tmp/data/", one_hot = True) 

import tensorflow as tf 
import matplotlib.pyplot as plt 

# Parameters 
learning_rate = 0.001 
training_epochs = 20 
batch_size = 100 
display_step = 1 

# Network Parameters 
n_hidden_1 = 256 

# 1st layer num features
n_hidden_2 = 256 # 2nd layer num features 
n_input = 784 # MNIST data input (img shape: 28*28) n_classes = 10 
# MNIST total classes (0-9 digits) 

# tf Graph input 
x = tf.placeholder("float", [None, n_input]) 
y = tf.placeholder("float", [None, n_classes]) 

# weights layer 1 
h = tf.Variable(tf.random_normal([n_input, n_hidden_1])) # bias layer 1 
bias_layer_1 = tf.Variable(tf.random_normal([n_hidden_1])) 
# layer 1 layer_1 = tf.nn.sigmoid(tf.add(tf.matmul(x, h), bias_layer_1)) 

# weights layer 2 
w = tf.Variable(tf.random_normal([n_hidden_1, n_hidden_2])) 

# bias layer 2 
bias_layer_2 = tf.Variable(tf.random_normal([n_hidden_2])) 

# layer 2 
layer_2 = tf.nn.sigmoid(tf.add(tf.matmul(layer_1, w), bias_layer_2)) 

# weights output layer 
output = tf.Variable(tf.random_normal([n_hidden_2, n_classes])) 

# biar output layer 
bias_output = tf.Variable(tf.random_normal([n_classes])) # output layer 
output_layer = tf.matmul(layer_2, output) + bias_output

# cost function 
cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(
   logits = output_layer, labels = y)) 

#cost = tf.reduce_mean(tf.nn.sigmoid_cross_entropy_with_logits(output_layer, y)) 
# optimizer 
optimizer = tf.train.AdamOptimizer(learning_rate = learning_rate).minimize(cost) 

# optimizer = tf.train.GradientDescentOptimizer(
   learning_rate = learning_rate).minimize(cost) 

# Plot settings 
avg_set = [] 
epoch_set = [] 

# Initializing the variables 
init = tf.global_variables_initializer() 

# Launch the graph 
with tf.Session() as sess: 
   sess.run(init) 
   
   # Training cycle
   for epoch in range(training_epochs): 
      avg_cost = 0. 
      total_batch = int(mnist.train.num_examples / batch_size) 
      
      # Loop over all batches 
      for i in range(total_batch): 
         batch_xs, batch_ys = mnist.train.next_batch(batch_size) 
         # Fit training using batch data sess.run(optimizer, feed_dict = {
            x: batch_xs, y: batch_ys}) 
         # Compute average loss 
         avg_cost += sess.run(cost, feed_dict = {x: batch_xs, y: batch_ys}) / total_batch
      # Display logs per epoch step 
      if epoch % display_step == 0: 
         print 
         Epoch:", '%04d' % (epoch + 1), "cost=", "{:.9f}".format(avg_cost)
      avg_set.append(avg_cost) 
      epoch_set.append(epoch + 1)
   print 
   "Training phase finished" 
   
   plt.plot(epoch_set, avg_set, 'o', label = 'MLP Training phase') 
   plt.ylabel('cost') 
   plt.xlabel('epoch') 
   plt.legend() 
   plt.show() 
   
   # Test model 
   correct_prediction = tf.equal(tf.argmax(output_layer, 1), tf.argmax(y, 1)) 
   
   # Calculate accuracy 
   accuracy = tf.reduce_mean(tf.cast(correct_prediction, "float")) 
   print 
   "Model Accuracy:", accuracy.eval({x: mnist.test.images, y: mnist.test.labels})

The above line of code generates the following output −

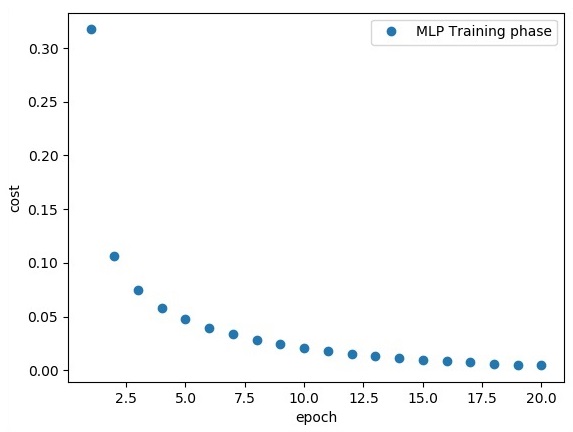
TensorFlow - Hidden Layers of Perceptron

In this chapter, we will be focus on the network we will have to learn from known set of points called x and f(x). A single hidden layer will build this simple network.

The code for the explanation of hidden layers of perceptron is as shown below −

#Importing the necessary modules 
import tensorflow as tf 
import numpy as np 
import math, random 
import matplotlib.pyplot as plt 

np.random.seed(1000) 
function_to_learn = lambda x: np.cos(x) + 0.1*np.random.randn(*x.shape) 
layer_1_neurons = 10 
NUM_points = 1000 

#Training the parameters 
batch_size = 100 
NUM_EPOCHS = 1500 

all_x = np.float32(np.random.uniform(-2*math.pi, 2*math.pi, (1, NUM_points))).T 
   np.random.shuffle(all_x) 

train_size = int(900) 
#Training the first 700 points in the given set x_training = all_x[:train_size] 
y_training = function_to_learn(x_training)

#Training the last 300 points in the given set x_validation = all_x[train_size:] 
y_validation = function_to_learn(x_validation) 

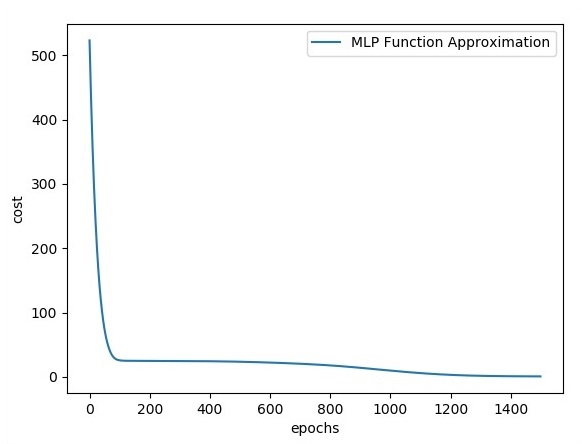
plt.figure(1) 
plt.scatter(x_training, y_training, c = 'blue', label = 'train') 
plt.scatter(x_validation, y_validation, c = 'pink', label = 'validation') 
plt.legend() 
plt.show()

X = tf.placeholder(tf.float32, [None, 1], name = "X")
Y = tf.placeholder(tf.float32, [None, 1], name = "Y")

#first layer 
#Number of neurons = 10 
w_h = tf.Variable(
   tf.random_uniform([1, layer_1_neurons],\ minval = -1, maxval = 1, dtype = tf.float32)) 
b_h = tf.Variable(tf.zeros([1, layer_1_neurons], dtype = tf.float32)) 
h = tf.nn.sigmoid(tf.matmul(X, w_h) + b_h)

#output layer 
#Number of neurons = 10 
w_o = tf.Variable(
   tf.random_uniform([layer_1_neurons, 1],\ minval = -1, maxval = 1, dtype = tf.float32)) 
b_o = tf.Variable(tf.zeros([1, 1], dtype = tf.float32)) 

#build the model 
model = tf.matmul(h, w_o) + b_o 

#minimize the cost function (model - Y) 
train_op = tf.train.AdamOptimizer().minimize(tf.nn.l2_loss(model - Y)) 

#Start the Learning phase 
sess = tf.Session() sess.run(tf.initialize_all_variables()) 

errors = [] 
for i in range(NUM_EPOCHS): 
   for start, end in zip(range(0, len(x_training), batch_size),\ 
      range(batch_size, len(x_training), batch_size)): 
      sess.run(train_op, feed_dict = {X: x_training[start:end],\ Y: y_training[start:end]})
   cost = sess.run(tf.nn.l2_loss(model - y_validation),\ feed_dict = {X:x_validation}) 
   errors.append(cost) 
   
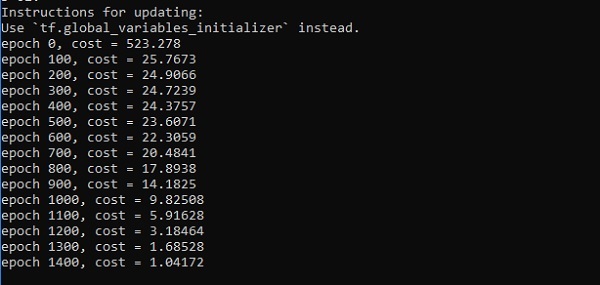
   if i%100 == 0: 
      print("epoch %d, cost = %g" % (i, cost)) 
      
plt.plot(errors,label='MLP Function Approximation') plt.xlabel('epochs') 
plt.ylabel('cost') 
plt.legend() 
plt.show()

Output

Following is the representation of function layer approximation −

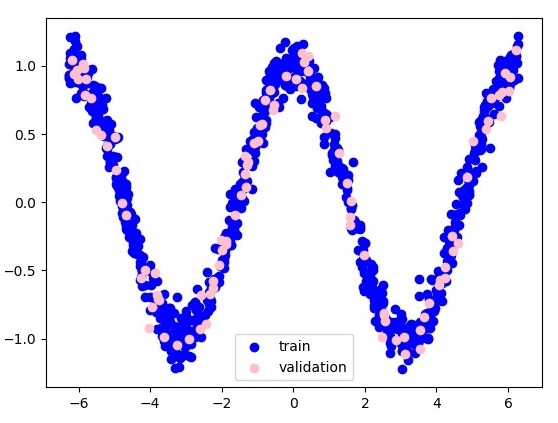
Here two data are represented in shape of W. The two data are: train and validation which are represented in distinct colors as visible in legend section.

TensorFlow - Optimizers

Optimizers are the extended class, which include added information to train a specific model. The optimizer class is initialized with given parameters but it is important to remember that no Tensor is needed. The optimizers are used for improving speed and performance for training a specific model.

The basic optimizer of TensorFlow is −

tf.train.Optimizer

This class is defined in the specified path of tensorflow/python/training/optimizer.py.

Following are some optimizers in Tensorflow −

Stochastic Gradient descent
Stochastic Gradient descent with gradient clipping
Momentum
Nesterov momentum
Adagrad
Adadelta
RMSProp
Adam
Adamax
SMORMS3

We will focus on the Stochastic Gradient descent. The illustration for creating optimizer for the same is mentioned below −

def sgd(cost, params, lr = np.float32(0.01)):
   g_params = tf.gradients(cost, params)
   updates = []
   
   for param, g_param in zip(params, g_params):
      updates.append(param.assign(param - lr*g_param))
   return updates

The basic parameters are defined within the specific function. In our subsequent chapter, we will focus on Gradient Descent Optimization with implementation of optimizers.

TensorFlow - XOR Implementation

In this chapter, we will learn about the XOR implementation using TensorFlow. Before starting with XOR implementation in TensorFlow, let us see the XOR table values. This will help us understand encryption and decryption process.

A	B	A XOR B
0	0	0
0	1	1
1	0	1
1	1	0

XOR Cipher encryption method is basically used to encrypt data which is hard to crack with brute force method, i.e., by generating random encryption keys which match the appropriate key.

The concept of implementation with XOR Cipher is to define a XOR encryption key and then perform XOR operation of the characters in the specified string with this key, which a user tries to encrypt. Now we will focus on XOR implementation using TensorFlow, which is mentioned below −

#Declaring necessary modules
import tensorflow as tf
import numpy as np
"""
A simple numpy implementation of a XOR gate to understand the backpropagation
algorithm
"""

x = tf.placeholder(tf.float64,shape = [4,2],name = "x")
#declaring a place holder for input x
y = tf.placeholder(tf.float64,shape = [4,1],name = "y")
#declaring a place holder for desired output y

m = np.shape(x)[0]#number of training examples
n = np.shape(x)[1]#number of features
hidden_s = 2 #number of nodes in the hidden layer
l_r = 1#learning rate initialization

theta1 = tf.cast(tf.Variable(tf.random_normal([3,hidden_s]),name = "theta1"),tf.float64)
theta2 = tf.cast(tf.Variable(tf.random_normal([hidden_s+1,1]),name = "theta2"),tf.float64)

#conducting forward propagation
a1 = tf.concat([np.c_[np.ones(x.shape[0])],x],1)
#the weights of the first layer are multiplied by the input of the first layer

z1 = tf.matmul(a1,theta1)
#the input of the second layer is the output of the first layer, passed through the 
   activation function and column of biases is added

a2 = tf.concat([np.c_[np.ones(x.shape[0])],tf.sigmoid(z1)],1)
#the input of the second layer is multiplied by the weights

z3 = tf.matmul(a2,theta2)
#the output is passed through the activation function to obtain the final probability

h3 = tf.sigmoid(z3)
cost_func = -tf.reduce_sum(y*tf.log(h3)+(1-y)*tf.log(1-h3),axis = 1)

#built in tensorflow optimizer that conducts gradient descent using specified 
   learning rate to obtain theta values

optimiser = tf.train.GradientDescentOptimizer(learning_rate = l_r).minimize(cost_func)

#setting required X and Y values to perform XOR operation
X = [[0,0],[0,1],[1,0],[1,1]]
Y = [[0],[1],[1],[0]]

#initializing all variables, creating a session and running a tensorflow session
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)

#running gradient descent for each iteration and printing the hypothesis 
   obtained using the updated theta values
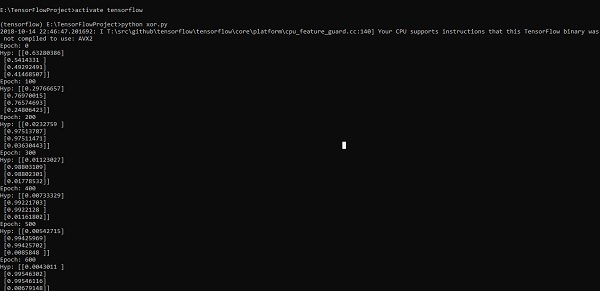
for i in range(100000):
   sess.run(optimiser, feed_dict = {x:X,y:Y})#setting place holder values using feed_dict
   if i%100==0:
      print("Epoch:",i)
      print("Hyp:",sess.run(h3,feed_dict = {x:X,y:Y}))

The above line of code generates an output as shown in the screenshot below −

TensorFlow - Gradient Descent Optimization

Gradient descent optimization is considered to be an important concept in data science.

Consider the steps shown below to understand the implementation of gradient descent optimization −

Step 1

Include necessary modules and declaration of x and y variables through which we are going to define the gradient descent optimization.

import tensorflow as tf

x = tf.Variable(2, name = 'x', dtype = tf.float32)
log_x = tf.log(x)
log_x_squared = tf.square(log_x)

optimizer = tf.train.GradientDescentOptimizer(0.5)
train = optimizer.minimize(log_x_squared)

Step 2

Initialize the necessary variables and call the optimizers for defining and calling it with respective function.

init = tf.initialize_all_variables()

def optimize():
   with tf.Session() as session:
      session.run(init)
      print("starting at", "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
      
      for step in range(10):
         session.run(train)
         print("step", step, "x:", session.run(x), "log(x)^2:", session.run(log_x_squared))
optimize()

The above line of code generates an output as shown in the screenshot below −

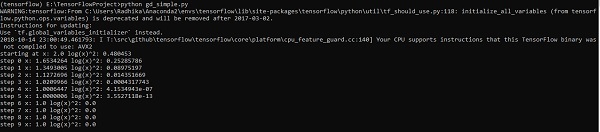
We can see that the necessary epochs and iterations are calculated as shown in the output.

TensorFlow - Forming Graphs

A partial differential equation (PDE) is a differential equation, which involves partial derivatives with unknown function of several independent variables. With reference to partial differential equations, we will focus on creating new graphs.

Let us assume there is a pond with dimension 500*500 square −

N = 500

Now, we will compute partial differential equation and form the respective graph using it. Consider the steps given below for computing graph.

Step 1 − Import libraries for simulation.

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt

Step 2 − Include functions for transformation of a 2D array into a convolution kernel and simplified 2D convolution operation.

def make_kernel(a):
   a = np.asarray(a)
   a = a.reshape(list(a.shape) + [1,1])
   return tf.constant(a, dtype=1)

def simple_conv(x, k):
   """A simplified 2D convolution operation"""
   x = tf.expand_dims(tf.expand_dims(x, 0), -1)
   y = tf.nn.depthwise_conv2d(x, k, [1, 1, 1, 1], padding = 'SAME')
   return y[0, :, :, 0]

def laplace(x):
   """Compute the 2D laplacian of an array"""
   laplace_k = make_kernel([[0.5, 1.0, 0.5], [1.0, -6., 1.0], [0.5, 1.0, 0.5]])
   return simple_conv(x, laplace_k)
   
sess = tf.InteractiveSession()

Step 3 − Include the number of iterations and compute the graph to display the records accordingly.

N = 500

# Initial Conditions -- some rain drops hit a pond

# Set everything to zero
u_init = np.zeros([N, N], dtype = np.float32)
ut_init = np.zeros([N, N], dtype = np.float32)

# Some rain drops hit a pond at random points
for n in range(100):
   a,b = np.random.randint(0, N, 2)
   u_init[a,b] = np.random.uniform()

plt.imshow(u_init)
plt.show()

# Parameters:
# eps -- time resolution
# damping -- wave damping
eps = tf.placeholder(tf.float32, shape = ())
damping = tf.placeholder(tf.float32, shape = ())

# Create variables for simulation state
U = tf.Variable(u_init)
Ut = tf.Variable(ut_init)

# Discretized PDE update rules
U_ = U + eps * Ut
Ut_ = Ut + eps * (laplace(U) - damping * Ut)

# Operation to update the state
step = tf.group(U.assign(U_), Ut.assign(Ut_))

# Initialize state to initial conditions
tf.initialize_all_variables().run()

# Run 1000 steps of PDE
for i in range(1000):
   # Step simulation
   step.run({eps: 0.03, damping: 0.04})
   
   # Visualize every 50 steps
   if i % 500 == 0:
      plt.imshow(U.eval())
      plt.show()

The graphs are plotted as shown below −

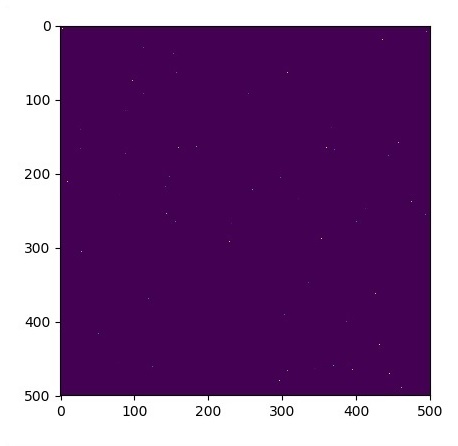
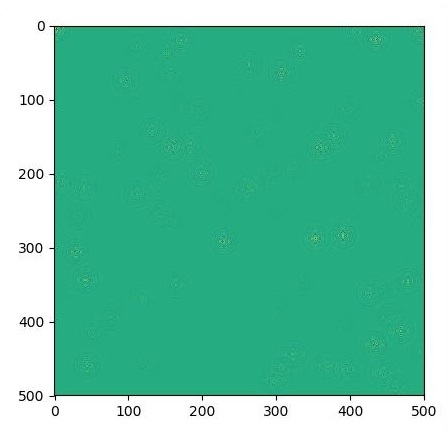
Image Recognition using TensorFlow

TensorFlow includes a special feature of image recognition and these images are stored in a specific folder. With relatively same images, it will be easy to implement this logic for security purposes.

The folder structure of image recognition code implementation is as shown below −

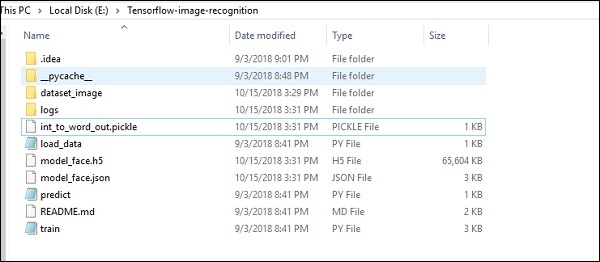
The dataset_image includes the related images, which need to be loaded. We will focus on image recognition with our logo defined in it. The images are loaded with “load_data.py” script, which helps in keeping a note on various image recognition modules within them.

import pickle
from sklearn.model_selection import train_test_split
from scipy import misc

import numpy as np
import os

label = os.listdir("dataset_image")
label = label[1:]
dataset = []

for image_label in label:
   images = os.listdir("dataset_image/"+image_label)
   
   for image in images:
      img = misc.imread("dataset_image/"+image_label+"/"+image)
      img = misc.imresize(img, (64, 64))
      dataset.append((img,image_label))
X = []
Y = []

for input,image_label in dataset:
   X.append(input)
   Y.append(label.index(image_label))

X = np.array(X)
Y = np.array(Y)

X_train,y_train, = X,Y

data_set = (X_train,y_train)

save_label = open("int_to_word_out.pickle","wb")
pickle.dump(label, save_label)
save_label.close()

The training of images helps in storing the recognizable patterns within specified folder.

import numpy
import matplotlib.pyplot as plt

from keras.layers import Dropout
from keras.layers import Flatten
from keras.constraints import maxnorm
from keras.optimizers import SGD
from keras.layers import Conv2D
from keras.layers.convolutional import MaxPooling2D
from keras.utils import np_utils
from keras import backend as K

import load_data
from keras.models import Sequential
from keras.layers import Dense

import keras
K.set_image_dim_ordering('tf')

# fix random seed for reproducibility
seed = 7
numpy.random.seed(seed)

# load data
(X_train,y_train) = load_data.data_set

# normalize inputs from 0-255 to 0.0-1.0
X_train = X_train.astype('float32')

#X_test = X_test.astype('float32')
X_train = X_train / 255.0

#X_test = X_test / 255.0
# one hot encode outputs
y_train = np_utils.to_categorical(y_train)

#y_test = np_utils.to_categorical(y_test)
num_classes = y_train.shape[1]

# Create the model
model = Sequential()
model.add(Conv2D(32, (3, 3), input_shape = (64, 64, 3), padding = 'same', 
   activation = 'relu', kernel_constraint = maxnorm(3)))

model.add(Dropout(0.2))
model.add(Conv2D(32, (3, 3), activation = 'relu', padding = 'same', 
   kernel_constraint = maxnorm(3)))

model.add(MaxPooling2D(pool_size = (2, 2)))
model.add(Flatten())
model.add(Dense(512, activation = 'relu', kernel_constraint = maxnorm(3)))
model.add(Dropout(0.5))
model.add(Dense(num_classes, activation = 'softmax'))

# Compile model
epochs = 10
lrate = 0.01
decay = lrate/epochs
sgd = SGD(lr = lrate, momentum = 0.9, decay = decay, nesterov = False)
model.compile(loss = 'categorical_crossentropy', optimizer = sgd, metrics = ['accuracy'])
print(model.summary())

#callbacks = [keras.callbacks.EarlyStopping(
   monitor = 'val_loss', min_delta = 0, patience = 0, verbose = 0, mode = 'auto')]
callbacks = [keras.callbacks.TensorBoard(log_dir='./logs', 
   histogram_freq = 0, batch_size = 32, write_graph = True, write_grads = False, 
   write_images = True, embeddings_freq = 0, embeddings_layer_names = None, 
   embeddings_metadata = None)]

# Fit the model

model.fit(X_train, y_train, epochs = epochs, 
   batch_size = 32,shuffle = True,callbacks = callbacks)

# Final evaluation of the model
scores = model.evaluate(X_train, y_train, verbose = 0)
print("Accuracy: %.2f%%" % (scores[1]*100))

# serialize model to JSONx
model_json = model.to_json()
with open("model_face.json", "w") as json_file:
   json_file.write(model_json)

# serialize weights to HDF5
model.save_weights("model_face.h5")
print("Saved model to disk")

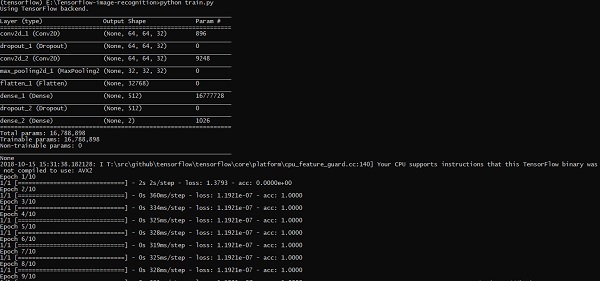
The above line of code generates an output as shown below −

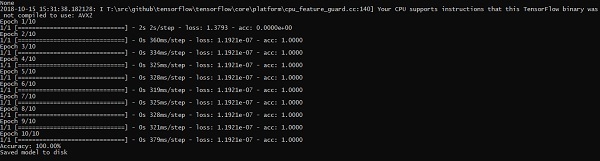
Recommendations for Neural Network Training

In this chapter, we will understand the various aspects of neural network training which can be implemented using TensorFlow framework.

Following are the ten recommendations, which can be evaluated −

Back Propagation

Back propagation is a simple method to compute partial derivatives, which includes the basic form of composition best suitable for neural nets.

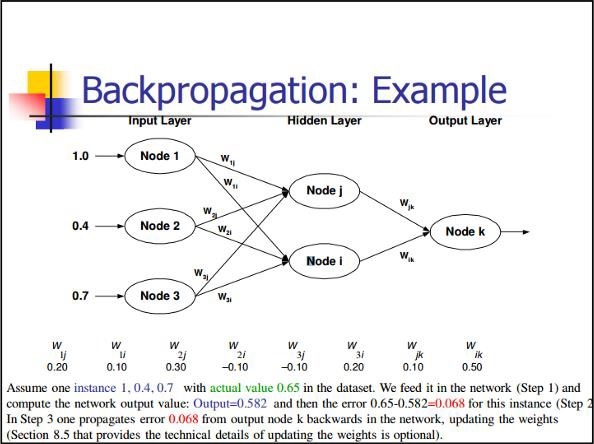
Stochastic Gradient Descent

In stochastic gradient descent, a batch is the total number of examples, which a user uses to calculate the gradient in a single iteration. So far, it is assumed that the batch has been the entire data set. The best illustration is working at Google scale; data sets often contain billions or even hundreds of billions of examples.

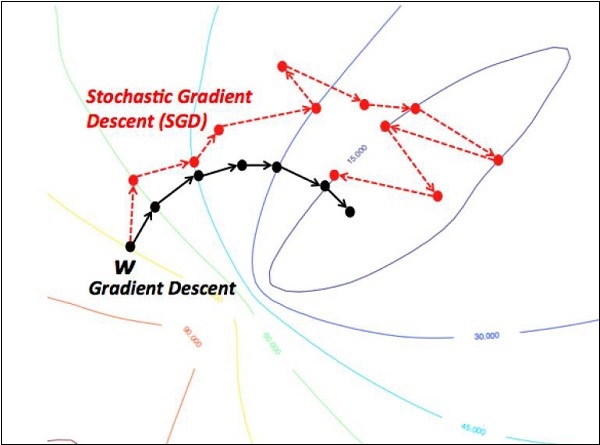
Learning Rate Decay

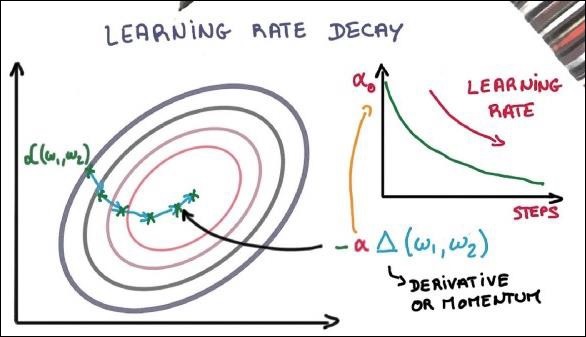
Adapting the learning rate is one of the most important features of gradient descent optimization. This is crucial to TensorFlow implementation.

Dropout

Deep neural nets with a large number of parameters form powerful machine learning systems. However, over fitting is a serious problem in such networks.

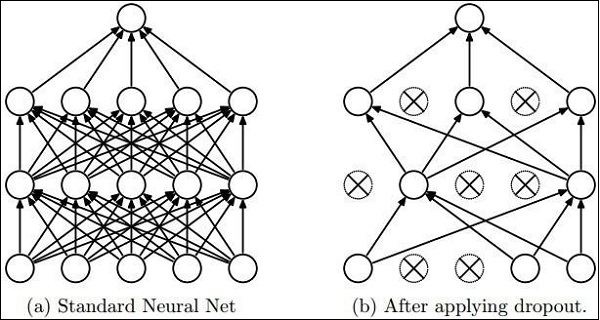
Max Pooling

Max pooling is a sample-based discretization process. The object is to down-sample an input representation, which reduces the dimensionality with the required assumptions.

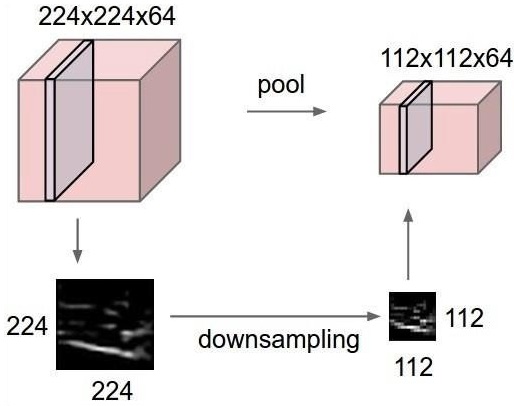
Long Short Term Memory (LSTM)

LSTM controls the decision on what inputs should be taken within the specified neuron. It includes the control on deciding what should be computed and what output should be generated.