
Functional Programming - Lambda Calculus
Lambda calculus is a framework developed by Alonzo Church in 1930s to study computations with functions.
Function creation − Church introduced the notation λx.E to denote a function in which x is a formal argument and E is the functional body. These functions can be of without names and single arguments.
Function application − Church used the notation E1.E2 to denote the application of function E1 to actual argument E2. And all the functions are on single argument.
Syntax of Lambda Calculus
Lamdba calculus includes three different types of expressions, i.e.,
E :: = x(variables)
| E1 E2(function application)
| λx.E(function creation)
Where λx.E is called Lambda abstraction and E is known as λ-expressions.
Evaluating Lambda Calculus
Pure lambda calculus has no built-in functions. Let us evaluate the following expression −
(+ (* 5 6) (* 8 3))
Here, we cant start with '+' because it only operates on numbers. There are two reducible expressions: (* 5 6) and (* 8 3).
We can reduce either one first. For example −
(+ (* 5 6) (* 8 3)) (+ 30 (* 8 3)) (+ 30 24) = 54
β-reduction Rule
We need a reduction rule to handle λs
(λx . * 2 x) 4 (* 2 4) = 8
This is called β-reduction.
The formal parameter may be used several times −
(λx . + x x) 4 (+ 4 4) = 8
When there are multiple terms, we can handle them as follows −
(λx . (λx . + ( x 1)) x 3) 9
The inner x belongs to the inner λ and the outer x belongs to the outer one.
(λx . + ( x 1)) 9 3 + ( 9 1) 3 + 8 3 = 11
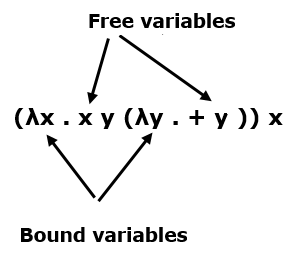
Free and Bound Variables
In an expression, each appearance of a variable is either "free" (to λ) or "bound" (to a λ).
β-reduction of (λx . E) y replaces every x that occurs free in E with y. For Example −
Alpha Reduction
Alpha reduction is very simple and it can be done without changing the meaning of a lambda expression.
λx . (λx . x) (+ 1 x) ↔ α λx . (λy . y) (+ 1 x)
For example −
(λx . (λx . + ( x 1)) x 3) 9 (λx . (λy . + ( y 1)) x 3) 9 (λy . + ( y 1)) 9 3 + ( 9 1) 3 + 8 3 11
Church-Rosser Theorem
The Church-Rosser Theorem states the following −
If E1 ↔ E2, then there exists an E such that E1 → E and E2 → E. Reduction in any way can eventually produce the same result.
If E1 → E2, and E2 is normal form, then there is a normal-order reduction of E1 to E2. Normal-order reduction will always produce a normal form, if one exists.