Texture Coordinate Function in Texture Mapping

---

---

At the heart of texture mapping, there is a concept of texture coordinate functions. These functions are important as they define how a 2D texture image is applied to a 3D surface. Read this chapter to learn the basics of texture coordinate functions and their role in texture mapping.

Texture Coordinate Functions

A texture coordinate function, typically denoted as , maps each point (x, y, z) on a 3D surface to a corresponding point (u, v) in 2D texture space. This mapping determines how the texture image is wrapped or applied to the 3D surface.

Key Properties of Effective Texture Coordinate Functions

Good texture coordinate functions should possess several important properties, as follows −

1. Bijectivity

Each point on the 3D surface should map to a unique point in texture space. This prevents multiple surface points from sharing the same texture coordinates.

In most cases, φ to be bijective, so that each point on the surface maps to a different point in texture space. The value at one point in the texture will affect several points on the surface. In cases where we want a texture to repeat over a surface, it needs a many-to-one mapping from surface points to texture points.

2. Low Size Distortion

The scale of the texture should remain relatively constant across the surface. This states that texture details appear consistent in size throughout the object. That is, close-together points anywhere on the surface that are about the same distance apart should map to points about the same distance apart in the texture. In terms of the function φ, the magnitude of the derivatives of φ should not vary too much.

3. Low Shape Distortion

The texture should not be excessively stretched or squeezed when applied to the surface. This preserves the original appearance of the texture. In terms of φ, the derivative of φ should not be too different in different directions.

Continuity

There should be minimal seams or discontinuities in the mapping. This helps maintain a smooth, natural look across the textured surface. That is, φ should be continuous, or have as few discontinuities as possible. In most cases, some discontinuities are inevitable, and we would like to put them in inconspicuous locations.

There are many approaches to defining texture coordinate functions. In the following sections, we will explain some of them in detail.

Geometrically Determined Coordinates

These methods compute texture coordinates based on the spatial coordinates of surface points. They are particularly useful for simple shapes or as initial mappings for more complex objects.

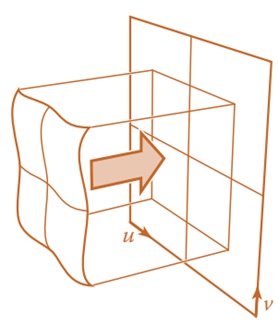
Planar Projection

Planar projection is one of the simplest methods. It uses a parallel projection, similar to orthographic viewing in 3D graphics.

The formula for planar projection is −

$$\mathrm{(x,y,z) \:=\: (u,v), \: where\:\: \begin{bmatrix}u \\ v \\ * \\ 1 \end{bmatrix} \:=\: M_t\: \begin{bmatrix}x \\ y \\ z \\ 1 \end{bmatrix}}$$

In this formula, M_t is an affine transformation matrix. Planar projection works good for surfaces that are mostly flat and don't have significant variations in surface normal.

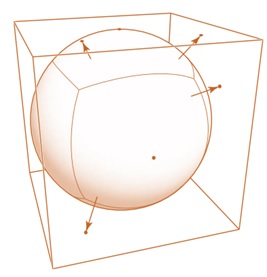
1. Spherical Coordinates

For objects that are roughly spherical in shape, we can use spherical coordinates. The formula for this method is −

$$\mathrm{\Phi(x, y, z) = \left( \frac{\pi + a \tan^2(y, x)}{2\pi}, \frac{\pi - a \cos\left( \frac{z}{|x|} \right)}{\pi} \right)}$$

This method projects points radially onto a sphere. It provides full coverage of the sphere but introduces distortion near the poles.

2. Cylindrical Coordinates

For objects that are more columnar in shape, cylindrical projection can be effective. The formula for cylindrical coordinates is −

$$\mathrm{\Phi(x,\: y,\: z) \:=\: \left( \frac{\frac{1}{2\pi}\left[\pi \:+\: \text{atan2}(y,\: x)\right]}{2\pi} , \frac{1}{2} \left[ 1 \:+\: z \right] \right)}$$

This method projects points outward from a central axis onto a cylinder.

3. Cubemaps

Cubemaps are an alternative to spherical projection that reduces distortion at the cost of introducing more seams. This method projects points onto the faces of a cube. The specific formula depends on which face of the cube a point projects onto.

Interpolated Texture Coordinates

For more precise control over texture mapping on triangle meshes, we can assign texture coordinates to each vertex and interpolate them across triangles. This method allows for fine-tuned control over how the texture is applied to complex surfaces.

• Visualizing Texture Coordinates − A common technique for visualizing texture coordinates is to draw mesh triangles in texture space. This method provides a clear view of which parts of the texture are used by different areas of the 3D model.
• Assessing Quality of Texture Coordinate Mappings − The quality of interpolated texture coordinates depends largely on how the mesh is laid out in texture space.
• Tiling and Wrapping Modes − In some cases, it's beneficial to allow texture coordinates to extend beyond the [0, 1] range. This technique can be used for various purposes −
  • Tiling textures across a surface
  • Focusing texture detail in specific areas of the model
  • Handling edge cases where rounding errors might push coordinates slightly out of bounds

Advanced Topics in Texture Coordinate Functions

Let us see some of the advanced topics of texture coordinate functions.

• Automatic Unwrapping − For complex models, manually defining texture coordinates can be time-consuming. Automatic unwrapping algorithms aim to generate good texture coordinates automatically. Sometimes by trying to minimize a combination of stretch and seam length.
• UV Layering − Some applications use multiple sets of texture coordinates for a single model. This allows different textures to be applied independently, such as a base color texture and a separate texture for weathering effects.
• Procedural Texture Coordinates − Instead of storing texture coordinates, some systems generate them procedurally. This can save memory and allow for dynamic effects, but may limit the level of control available to artists.

Conclusion

In this chapter, we discussed the role of texture coordinate functions in computer graphics. We highlighted its importance in effective texture mapping. We understood various types of texture coordinate functions, including geometrically determined methods like planar projection, spherical coordinates, cylindrical coordinates, and cubemaps.

We also discussed the use of interpolated texture coordinates for more complex triangle meshes. Additionally, we saw practical considerations such as visualizing texture coordinates and assessing mapping quality. Finally, we understood some advanced topics in the field.