- Accounting - Home
- Accounting - Overview
- Accounting - Process
- Accounting - Basic Concepts
- Accounting - Conventions
- Accounting - Accounts' Classification
- Accounting - Systems
- Financial Accounting - Journal
- Financial Accounting - Ledger
- Financial Accounting - Books
- Financial Accounting - Depreciation
- Cost Accounting
- Cost Accounting - Introduction
- Cost Accounting - Advantages
- Cost Accounting - vs. Financial A/c
- Cost Accounting - Cost Classification
- Cost Accounting - Elements of Cost
- Cost Accounting - Cost Sheet
- Cost Accounting - Cost Control
- Cost Accounting - Cost Reduction
- Cost Accounting - Budgeting
- Cost Accounting Techniques
- Cost Accounting - Marginal Costing
- Cost Accounting - Standard Costing
- Cost Accounting - Variance Analysis
- Cost Accounting - CVP Analysis
- Management Accounting
- Management A/c - Introduction
- Management A/c - vs. Cost A/c
- Management A/c - vs. Financial A/c
- Management A/c - Cash Flow
- Management A/c - Ratio Analysis
- Management A/c - Useful Ratios
- Management A/c - Working Capital
- Accounting Useful Resources
- Accounting Basics - Quick Guide
- Accounting Basics - Useful Resources
Cost Accounting - CVP Analysis
Cost-Volume-Profit (CVP) Analysis is also known as BreakEven Analysis. Every business organization works to maximize its profits. With the help of CVP analysis, the management studies the co-relation of profit and the level of production.
CVP analysis is concerned with the level of activity where total sales equals the total cost and it is called as the break-even point. In other words, we study the sales value, cost and profit at different levels of production. CVP analysis highlights the relationship between the cost, the sales value, and the profit.
Assumptions
Let us go through the assumptions for CVP analysis:
Variable costs remain variable and fixed costs remain static at every level of production.
Sales volume does not affect the selling price of the product. We can assume the selling price as constant.
At all level of sales, the volume, material, and labor costs remain constant.
Efficiency and productivity remains unchanged at all the levels of sales volume.
The sales-mix at all level of sales remains constant in a multi-product situation.
The relevant factor which affects the cost and revenue is volume only.
The volume of sales is equal to the volume of production.
Marginal Cost Equation
Equations for elements of cost are as follows:
Sales = Variable costs + Fixed Expenses Profit /Loss
Or
Sales Variable Cost = Fixed Expenses Profit /Loss
Or
Sales Variable Cost = Contribution
It is necessary to understand the following four concepts, their calculations, and applications to know the mathematical relation between cost, volume, and profit:
- Contribution
- Profit Volume Ratio (P/V Ratio or Contribution/Sales (C/S))
- Break-Even Point
- Margin of Safety
Contribution
Contribution = Sales Marginal Cost
We have already discussed contribution in Marginal Costing topic above.
Profit-Volume Ratio
Profit / Volume (P/V) ratio is calculated while studying the profitability of operations of a business and to establish a relation between Sales and Contribution. It is one of the most important ratios, calculated as under:
The P/V Ratio shares a direct relation with profits. Higher the P/V ratio, more the profit and vice-a-versa.
Break-Even Point
When the total cost of executing business equals to the total sales, it is called break-even point. Contribution equals to the fixed cost at this point. Here is a formula to calculate break-even point:
Break-even point based on total sales:
Calculation of output or sales value at which a desired profit is earned:
Composite Break Even Point
A company may have different production units, where they may produce the same product. In this case, the combined fixed cost of each productions unit and the combined total sales are taken into consideration to find out BEP.
Constant Product - Mix Approach In this approach, the ratio is constant for the products of all production units.
Variable Product - Mix Approach In this approach, the preference of products is based on bigger ratio.
Margin of Safety
Excess of sale at BEP is known as margin of safety. Therefore,
Margin of safety = Actual Sales − Sales at BEP
Margin of safety may be calculated with the help of the following formula:
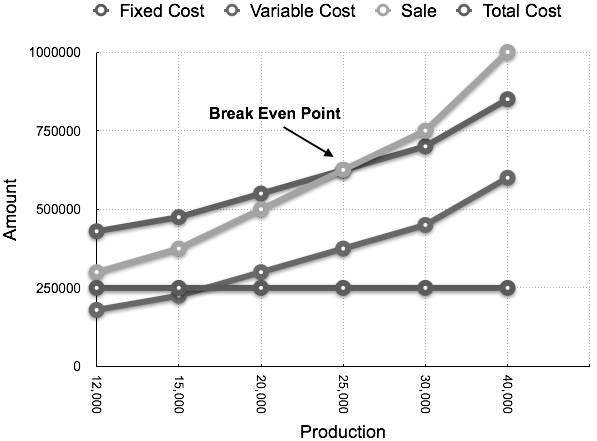
Break-Even Chart
Break-Even Chart is the most useful graphical representation of marginal costing. It converts accounting data to a useful readable report. Estimated profits, losses, and costs can be determined at different levels of production. Let us take an example.
Example
Calculate break-even point and draw the break-even chart from the following data:
Fixed Cost = Rs 2,50,000 Variable Cost = Rs 15 per unit Selling Price = Rs 25 per unit Production level in units 12,000, 15,000, 20,000, 25,000, 30,000, and 40,000.
Solution:
At production level of 25,000 units, the total cost will be Rs 6,25,000.
(Calculated as (25000 × 14) + 2,50000)
| Statement showing Profit & Margin of safety at different level of production Break Even Sale = Rs 6,25,000 (25,000 x 25) | ||||
| Production (In Units) |
Total Sale (In Rs) |
Total Cost (In Rs) |
Profit (Sales - Cost) (In Rs) |
Margin of safety (Profit/Contribution per unit) (In Units) |
| 12000 | 3,00,000 | 4,30,000 | -1,30,000 | |
| 15000 | 3,75,000 | 4,75,000 | -1,00,000 | |
| 20000 | 5,00,000 | 5,50,000 | -50,000 | |
| 25000 | 6,25,000 | 6,25,000 | (B.E.P) | (B.E.P) |
| 30000 | 7,50,000 | 7,00,000 | 50,000 | 5,000 |
| 40000 | 10,00,000 | 8,50,000 | 1,50,000 | 15,000 |
The corresponding chart plotted as production against amount appears as follows: