
- Digital Electronics - Home
- Digital Electronics Basics
- Types of Digital Systems
- Types of Signals
- Logic Levels And Pulse Waveforms
- Digital System Components
- Digital Logic Operations
- Digital Systems Advantages
- Number Systems
- Number Systems
- Binary Numbers Representation
- Binary Arithmetic
- Signed Binary Arithmetic
- Octal Arithmetic
- Hexadecimal Arithmetic
- Complement Arithmetic
- Base Conversions
- Base Conversions
- Binary to Decimal Conversion
- Decimal to Binary Conversion
- Binary to Octal Conversion
- Octal to Binary Conversion
- Octal to Decimal Conversion
- Decimal to Octal Conversion
- Hexadecimal to Binary Conversion
- Binary to Hexadecimal Conversion
- Hexadecimal to Decimal Conversion
- Decimal to Hexadecimal Conversion
- Octal to Hexadecimal Conversion
- Hexadecimal to Octal Conversion
- Binary Codes
- Binary Codes
- 8421 BCD Code
- Excess-3 Code
- Gray Code
- ASCII Codes
- EBCDIC Code
- Code Conversion
- Error Detection & Correction Codes
- Logic Gates
- Logic Gates
- AND Gate
- OR Gate
- NOT Gate
- Universal Gates
- XOR Gate
- XNOR Gate
- CMOS Logic Gate
- OR Gate Using Diode Resistor Logic
- AND Gate vs OR Gate
- Two Level Logic Realization
- Threshold Logic
- Boolean Algebra
- Boolean Algebra
- Laws of Boolean Algebra
- Boolean Functions
- DeMorgan's Theorem
- SOP and POS Form
- POS to Standard POS Form
- Minimization Techniques
- K-Map Minimization
- Three Variable K-Map
- Four Variable K-Map
- Five Variable K-Map
- Six Variable K-Map
- Don't Care Condition
- Quine-McCluskey Method
- Min Terms and Max Terms
- Canonical and Standard Form
- Max Term Representation
- Simplification using Boolean Algebra
- Combinational Logic Circuits
- Digital Combinational Circuits
- Digital Arithmetic Circuits
- Multiplexers
- Multiplexer Design Procedure
- Mux Universal Gate
- 2-Variable Function Using 4:1 Mux
- 3-Variable Function Using 8:1 Mux
- Demultiplexers
- Mux vs Demux
- Parity Bit Generator and Checker
- Comparators
- Encoders
- Keyboard Encoders
- Priority Encoders
- Decoders
- Arithmetic Logic Unit
- 7-Segment LED Display
- Code Converters
- Code Converters
- Binary to Decimal Converter
- Decimal to BCD Converter
- BCD to Decimal Converter
- Binary to Gray Code Converter
- Gray Code to Binary Converter
- BCD to Excess-3 Converter
- Excess-3 to BCD Converter
- Adders
- Half Adders
- Full Adders
- Serial Adders
- Parallel Adders
- Full Adder using Half Adder
- Half Adder vs Full Adder
- Full Adder with NAND Gates
- Half Adder with NAND Gates
- Binary Adder-Subtractor
- Subtractors
- Half Subtractors
- Full Subtractors
- Parallel Subtractors
- Full Subtractor using 2 Half Subtractors
- Half Subtractor using NAND Gates
- Sequential Logic Circuits
- Digital Sequential Circuits
- Clock Signal and Triggering
- Latches
- Shift Registers
- Shift Register Applications
- Binary Registers
- Bidirectional Shift Register
- Counters
- Binary Counters
- Non-binary Counter
- Design of Synchronous Counter
- Synchronous vs Asynchronous Counter
- Finite State Machines
- Algorithmic State Machines
- Flip Flops
- Flip-Flops
- Conversion of Flip-Flops
- D Flip-Flops
- JK Flip-Flops
- T Flip-Flops
- SR Flip-Flops
- Clocked SR Flip-Flop
- Unclocked SR Flip-Flop
- Clocked JK Flip-Flop
- JK to T Flip-Flop
- SR to JK Flip-Flop
- Triggering Methods:Flip-Flop
- Edge-Triggered Flip-Flop
- Master-Slave JK Flip-Flop
- Race-around Condition
- A/D and D/A Converters
- Analog-to-Digital Converter
- Digital-to-Analog Converter
- DAC and ADC ICs
- Realization of Logic Gates
- NOT Gate from NAND Gate
- OR Gate from NAND Gate
- AND Gate from NAND Gate
- NOR Gate from NAND Gate
- XOR Gate from NAND Gate
- XNOR Gate from NAND Gate
- NOT Gate from NOR Gate
- OR Gate from NOR Gate
- AND Gate from NOR Gate
- NAND Gate from NOR Gate
- XOR Gate from NOR Gate
- XNOR Gate from NOR Gate
- NAND/NOR Gate using CMOS
- Full Subtractor using NAND Gate
- AND Gate Using 2:1 MUX
- OR Gate Using 2:1 MUX
- NOT Gate Using 2:1 MUX
- Memory Devices
- Memory Devices
- RAM and ROM
- Cache Memory Design
- Programmable Logic Devices
- Programmable Logic Devices
- Programmable Logic Array
- Programmable Array Logic
- Field Programmable Gate Arrays
- Digital Electronics Families
- Digital Electronics Families
- CPU Architecture
- CPU Architecture
What is Excess-3 Code?
Excess-3 code is a non-weighted BCD (Binary Coded Decimal) code. It is called excess-3 code because it is obtained by adding 0011 (3) to the 8421 BCD code. Also called XS-3, the excess 3 code is a BCD code that represents each decimal digit as a 4-bit binary code.
The excess-3 binary code is a sequential code, so we can use it to perform arithmetic operations. Also, it is a self-complementing code, therefore the subtraction operation by the complement method is simpler than that in the 8421 BCD code.
However, in the excess-3 code, there are six invalid codes, they are 0000, 0001, 0010, 1110, and 1111.
How to Obtain Excess-3 Code?
We can obtain the excess-3 code by adding 0011 (3) to the natural 8421 BCD code. It is explained here −
Decimal digit = 0 8421 BCD code = 0000 Excess-3 code = 0000 + 0011 = 0011 Decimal digit = 1 8421 BCD code = 0001 Excess-3 code = 0001 + 0011 = 0100
Similarly, we can obtain the excess-3 code for all the decimal digits.
The following table shows the excess-3 code for each decimal digit −
| Decimal Digit | Excess-3 Code |
|---|---|
| 0 | 0011 |
| 1 | 0100 |
| 2 | 0101 |
| 3 | 0110 |
| 4 | 0111 |
| 5 | 1000 |
| 6 | 1001 |
| 7 | 1010 |
| 8 | 1011 |
| 9 | 1100 |
Note − The Excess-3 code is not so widely used today. It was mainly used in early digital systems. Nowadays, many other advanced and efficient binary codes are being used in place of the excess-3 code.
Importance of Excess-3 Code in Digital Electronics
Excess-3 code is one of the widely used binary codes in early digital systems. Here are some of the key reasons why excess-3 code was used in the field of digital electronics −
- It provides a simplified way of converting a decimal number into binary code.
- It has self-complementing property that makes it suitable for error detection and correction applications.
- It is sequential code, hence it can be used to perform arithmetic operations in digital systems.
- Excess-3 code is highly compatible with decimal IO devices. Thus, it provides a convenient interface between digital systems and other devices.
Advantages of Excess-3 Code
Although, the excess-3 code is less common in modern digital systems. But it has the following key benefits over other binary coding schemes −
- Excess-3 code provides an easy method of representing decimal numbers in binary form.
- Excess-3 code provides an easier way of performing addition and subtraction operations without using any complex conversion methods.
- Excess-3 code is quite easy to convert to and from decimal numbers.
- Excess-3 code being a binary-coded decimal is highly compatible with a wide range of decimal devices.
Disadvantages of Excess-3 Code
Excess-3 code has several advantages, but it also has certain disadvantages as well thats why it is less commonly used in modern digital systems. The following are some key disadvantages of excess-3 code −
- Excess-3 code is an inefficient binary representation of decimal numbers as compared to pure binary. This is because it requires more bits to represent a decimal digit.
- Excess-3 code requires additional arithmetic circuit to add 3 to the standard binary code.
- Excess-3 code has limited compatibility with pure binary systems.
Applications of Excess-3 Code
Excess-3 code was widely used in early digital systems and digital computers. The key areas of excess-3 code applications are listed below −
- Excess-3 code was used in early digital computers.
- Excess-3 code is also used in decimal data processing through digital systems.
- Excess-3 code is also used in digital devices likes printers, card readers, etc. where decimal data is employed.
- The self-complementing property of excess-3 code makes it suitable to use in error detection and correction applications.
- Excess-3 code is also communication and data transmission applications.
Excess-3 Addition
In excess-3 addition, starting from LSD (least significant digit), we add the 4-bit group in each column.
If no end-around carry is generated from the addition of 4-bit group, we have to subtract 0011 from the sum term to obtain the result. This is because, no carry means the result is in XS-6 format. Thus, we obtain the correct sum by adding 0011 to the sum term.
If an end-around carry is produced from the addition, we have to add 0011 to the sum term to obtain the corrected result. This is because the carry out represents that the sum term is an invalid excess-3 code, which is corrected by adding 0011 to the sum term.
Let us understand the XS-3 addition with the help of examples.
Example
Add 35 and 28 in XS-3 code.
Solution
The given decimal numbers and their XS-3 code are
35 = 0110 1000
28 = 0101 1011
Adding the XS-3 codes,
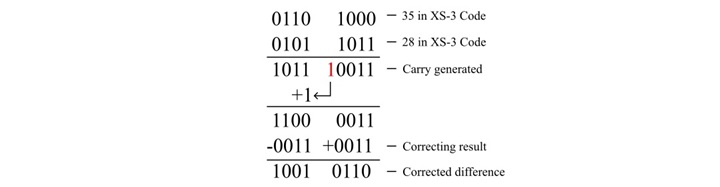
Hence, the correct sum of 35 and 28 is 1001 0110 in XS-3 and 63 in decimal.
Excess-3 Subtraction
In the XS-3 subtraction, starting from the least significant digit, we find the difference of two numbers by subtracting each group of 4-bits of subtrahend from he corresponding 4-bit group of the minuend.
In the XS-3 subtraction, if there is no borrow from the higher 4-bit group, then we add 0011 to the difference term to obtain the corrected result. This is because if there is no borrow, then the result is in the normal binary that has to be converted into XS-3 by adding 0011 to it.
If a borrow is taken from the next 4-bit group, then the difference term will be an invalid XS-3 code which is corrected by subtracting 0011 from it.
Let us understand the XS-3 subtraction through a solved example.
Example
Subtract 28 from 56 in XS-3 code.
Solution
Given,
Minuend = (56)10 = (1000 1001)XS-3
Subtrahend = (28)10 = (0101 1011)XS-3
Subtracting in the XS-3 code, we get,

Hence, the corrected difference of the numbers 56 and 28 is 0101 1011 in XS-3 code and 28 in decimal.
Conclusion
In conclusion, the Excess-3 (XS-3) code is a binary coding scheme widely used in old digital systems. It is basically a BCD scheme used to represent decimal digits in binary format.
In modern digital systems, the excess-3 code is replaced by more efficient binary codes like 8421 BCD code, ASCII code, etc.