Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Unsigned and Signed Binary Numbers
Variables such as integers can be represent in two ways, i.e., signed and unsigned. Signed numbers use sign flag or can be distinguish between negative values and positive values. Whereas unsigned numbers stored only positive numbers but not negative numbers.
Number representation techniques like: Binary, Octal, Decimal, and Hexadecimal number representation techniques can represent numbers in both signed and unsigned ways. Binary Number System is one the type of Number Representation techniques. It is most popular and used in digital systems. Binary system is used for representing binary quantities which can be represented by any device that has only two operating states or possible conditions. For example, a switch has only two states: open or close.
In the Binary System, there are only two symbols or possible digit values, i.e., 0 and 1. Represented by any device that only 2 operating states or possible conditions. Binary numbers are indicated by the addition of either an 0b prefix or an 2 suffix.
Representation of Binary Numbers:
Binary numbers can be represented in signed and unsigned way. Unsigned binary numbers do not have sign bit, whereas signed binary numbers uses signed bit as well or these can be distinguishable between positive and negative numbers. A signed binary is a specific data type of a signed variable.
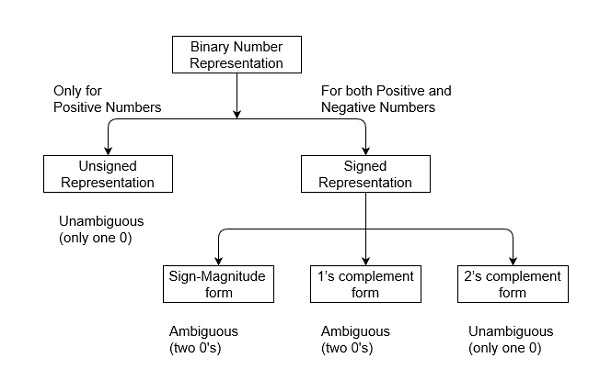
1. Unsigned Numbers:
Unsigned numbers don’t have any sign, these can contain only magnitude of the number. So, representation of unsigned binary numbers are all positive numbers only. For example, representation of positive decimal numbers are positive by default. We always assume that there is a positive sign symbol in front of every number.
Representation of Unsigned Binary Numbers:
Since there is no sign bit in this unsigned binary number, so N bit binary number represent its magnitude only. Zero (0) is also unsigned number. This representation has only one zero (0), which is always positive. Every number in unsigned number representation has only one unique binary equivalent form, so this is unambiguous representation technique. The range of unsigned binary number is from 0 to (2n-1).
Example-1: Represent decimal number 92 in unsigned binary number.
Simply convert it into Binary number, it contains only magnitude of the given number.
= (92)10
= (1x26+0x25+1x24+1x23+1x22+0x21+0x20)10
= (1011100)2
It’s 7 bit binary magnitude of the decimal number 92.
Example-2: Find range of 5 bit unsigned binary numbers. Also, find minimum and maximum value in this range.
Since, range of unsigned binary number is from 0 to (2n-1). Therefore, range of 5 bit unsigned binary number is from 0 to (25-1) which is equal from minimum value 0 (i.e., 00000) to maximum value 31 (i.e., 11111).
2. Signed Numbers:
Signed numbers contain sign flag, this representation distinguish positive and negative numbers. This technique contains both sign bit and magnitude of a number. For example, in representation of negative decimal numbers, we need to put negative symbol in front of given decimal number.
Representation of Signed Binary Numbers:
There are three types of representations for signed binary numbers. Because of extra signed bit, binary number zero has two representation, either positive (0) or negative (1), so ambiguous representation. But 2’s complementation representation is unambiguous representation because of there is no double representation of number 0. These are: Sign-Magnitude form, 1’s complement form, and 2’s complement form which are explained as following below.
2.(a) Sign-Magnitude form:
For n bit binary number, 1 bit is reserved for sign symbol. If the value of sign bit is 0, then the given number will be positive, else if the value of sign bit is 1, then the given number will be negative. Remaining (n-1) bits represent magnitude of the number. Since magnitude of number zero (0) is always 0, so there can be two representation of number zero (0), positive (+0) and negative (-0), which depends on value of sign bit. Hence these representations are ambiguous generally because of two representation of number zero (0). Generally sign bit is a most significant bit (MSB) of representation. The range of Sign-Magnitude form is from (2(n-1)-1) to (2(n-1)-1).
For example, range of 6 bit Sign-Magnitude form binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i.e., 1 11111) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 00000) and +0 (i.e., 0 00000).
2.(b) 1’s complement form:
Since, 1’s complement of a number is obtained by inverting each bit of given number. So, we represent positive numbers in binary form and negative numbers in 1’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 1’s complement of given binary number. You can get negative number by 1’s complement of a positive number and positive number by using 1’s complement of a negative number. Therefore, in this representation, zero (0) can have two representation, that’s why 1’s complement form is also ambiguous form. The range of 1’s complement form is from (2(n-1)-1) to (2(n-1)-1) .
For example, range of 6 bit 1’s complement form binary number is from (25-1) to (25-1) which is equal from minimum value -31 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 11111) and +0 (i.e., 0 00000).
2.(c) 2’s complement form:
Since, 2’s complement of a number is obtained by inverting each bit of given number plus 1 to least significant bit (LSB). So, we represent positive numbers in binary form and negative numbers in 2’s complement form. There is extra bit for sign representation. If value of sign bit is 0, then number is positive and you can directly represent it in simple binary form, but if value of sign bit 1, then number is negative and you have to take 2’s complement of given binary number. You can get negative number by 2’s complement of a positive number and positive number by directly using simple binary representation. If value of most significant bit (MSB) is 1, then take 2’s complement from, else not. Therefore, in this representation, zero (0) has only one (unique) representation which is always positive. The range of 2’s complement form is from (2(n-1)) to (2(n-1)-1).
For example, range of 6 bit 2’s complement form binary number is from (25) to (25-1) which is equal from minimum value -32 (i.e., 1 00000) to maximum value +31 (i.e., 0 11111). And zero (0) has two representation, -0 (i.e., 1 11111) and +0 (i.e., 0 00000).
44K+ Views
