Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Pizza With 3n Slices in C++
Suppose there is a pizza with 3n slices of varying size, I and my two friends will take slices of pizza as follows −
I shall pick any pizza slice.
My friend Amal will pick next slice in anti clockwise direction of my pick.
My friend Bimal will pick next slice in clockwise direction of my pick.
Repeat these steps until there are no more slices of pizzas.
Sizes of Pizza slices is represented by circular array slices in clockwise direction. We have to find the maximum possible sum of slice sizes which I can have.
So, if the input is like [9,8,6,1,1,8],
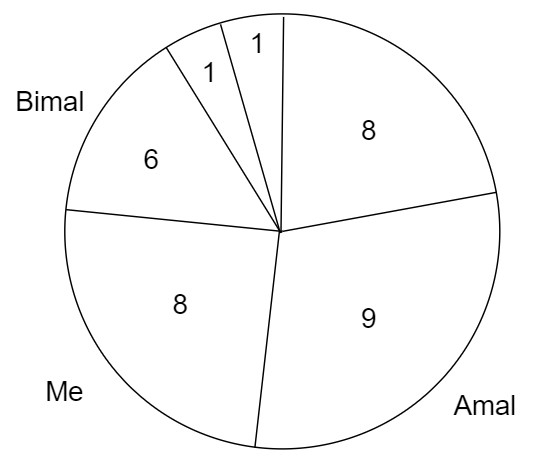
then the output will be 16, as pick pizza slice of size 8 in each turn. If I pick slice with size 9 my friends will pick slices of size 8.
To solve this, we will follow these steps −
Define a function solve(), this will take an array v, and one argument m,
n := size of v
Define two 2D arrays dp1 and dp2 of size (n + 1) x (m + 1) each
for initialize i := 0, when i < n, update (increase i by 1), do −
for initialize j := 0, when j <= m, update (increase j by 1), do −
x := v[i]
if j < m, then −
dp2[i + 1, j + 1] = maximum of dp2[i + 1, j + 1] and dp1[i, j] + x)
dp1[i + 1, j] = maximum of dp1[i + 1, j], dp2[i, j] and dp1[i, j]
return maximum of dp1[n, m] and dp2[n, m]
From the main method do the following −
n := size of slices
ret := 0
ret := maximum of solve(slices from index 1 to end, n/3) and slices[0] + solve(slices from index 2 to end - 1, n/3 - 1)
return ret
Let us see the following implementation to get better understanding −
Example
#include <bits/stdc++.h>
using namespace std;
class Solution {
public:
int solve(vector <int> v, int m){
int n = v.size();
vector<vector<int> > dp1(n + 1, vector<int>(m + 1));
vector<vector<int> > dp2(n + 1, vector<int>(m + 1));
for (int i = 0; i < n; i++) {
for (int j = 0; j <= m; j++) {
int x = v[i];
if (j < m)
dp2[i + 1][j + 1] = max(dp2[i + 1][j + 1], dp1[i]
[j] + x);
dp1[i + 1][j] = max({ dp1[i + 1][j], dp2[i][j],
dp1[i][j] });
}
}
return max(dp1[n][m], dp2[n][m]);
}
int maxSizeSlices(vector<int>& slices) {
int n = slices.size();
int ret = 0;
ret = max(solve(vector<int>(slices.begin() + 1,
slices.end()), n / 3), slices[0] + solve(vector<int>(slices.begin() +
2, slices.end() - 1), n / 3 - 1));
return ret;
}
};
main(){
Solution ob;
vector<int> v = {9,8,6,1,1,8};
cout << (ob.maxSizeSlices(v));
}Input
{9,8,6,1,1,8}Output
16
246 Views
