Pascal's Triangle Printing In C

Pascal's triangle is one of the classic example taught to engineering students. It has many interpretations. One of the famous one is its use with binomial equations.

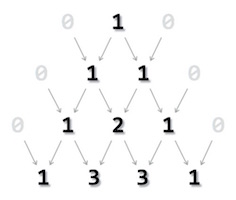
All values outside the triangle are considered zero (0). The first row is 0 1 0 whereas only 1 acquire a space in pascal's triangle, 0s are invisible. Second row is acquired by adding (0+1) and (1+0). The output is sandwiched between two zeroes. The process continues till the required level is achieved.

Pascal's triangle can be derived using binomial theorem. We can use combinations and factorials to achieve this.

Algorithm

Assuming that we're well aware of factorials, we shall look into the core concept of drawing a pascal triangle in step-by-step fashion −

START
  Step  1 - Take number of rows to be printed, n.
  Step  2 - Make outer iteration I for n times to print rows
  Step  3 - Make inner iteration for J to (N - 1)
  Step  4 - Print single blank space " "
  Step  5 - Close inner loop
  Step  6 - Make inner iteration for J to I
  Step  7 - Print nCr of I and J
  Step  8 - Close inner loop
  Step  9 - Print NEWLINE character after each inner iteration
  Step 10 - Return
STOP

Pseudocode

We can derive a pseudocode for the above mentioned algorithm, as follows −

procedure pascals_triangle

   FOR I = 0 to N DO
      FOR J = 0 to N-1 DO
         PRINT " "
      END FOR

      FOR J = 0 to I DO
         PRINT nCr(i,j)
      END FOR

      PRINT NEWLINE
   END FOR

end procedure

Implementation

Let's implement this program in full length. We shall implement functions for factorial (non-recursive) as well ncr (combination).

#include <stdio.h>

int factorial(int n) {
   int f;
   
   for(f = 1; n > 1; n--)
      f *= n;
      
   return f;
}

int ncr(int n,int r) {
   return factorial(n) / ( factorial(n-r) * factorial(r) );
}

int main() {
   int n, i, j;

   n = 5;

   for(i = 0; i <= n; i++) {
      for(j = 0; j <= n-i; j++)
         printf("  ");
         
      for(j = 0; j <= i; j++)
         printf(" %3d", ncr(i, j));

      printf("\n");
   }
   return 0;
}

The output should look like this −

               1
             1   1
           1   2   1
         1   3   3   1
       1   4   6   4   1
     1   5  10  10   5   1

Kickstart Your Career

Get certified by completing the course

Get Started