Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
Cheapest Flights Within K Stops in C++
Suppose we have n cities connected by m flights. Each flight starts from u and arrives at v with a price w. If we have all the cities and flights, together with starting city src and the destination dst, here our task is to find the cheapest price from src to dst with up to k stops. If there is no such route, then return -1.
So, if the input is like n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]], src = 0, dst = 2, k = 1, then the output will be 200
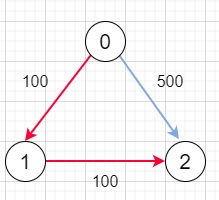
To solve this, we will follow these steps −
Create one data structure called Data, this can hold node, dist and val
Define one 2D array cost
cost := one 2D array of order (n + 1) x (K + 10) fill this with infinity
Define one 3D array graph
for initialize i := 0, when i < size of flights, update (increase i by 1), do −
u := flights[i, 0]
v := flights[i, 1]
insert { v, flights[i, 2] } at the end of graph[u]
define one priority queue q
insert Data(src, 0, 0) into q
cost[src, 0] := 0
ans := -1
while (not q is empty), do −
temp := top element of q
curr := temp.node
delete element from q
dist := temp.dist
if curr is same as dst, then −
return temp.cost
(increase dist by 1)
if dist > K + 1, then −
Ignore following part, skip to the next iteration
for initialize i := 0, when i < size of graph[curr], update (increase i by 1), do −
neighbour := graph[curr, i, 0]
if cost[neighbour, dist] > cost[curr, dist - 1] + graph[curr, i, 1], then −
cost[neighbour, dist] := cost[curr, dist - 1] + graph[curr, i, 1]
insert Data(neighbour, dist, cost[neighbour, dist]) into q
return -1
Example
Let us see the following implementation to get better understanding −
#include <bits/stdc++.h>
using namespace std;
struct Data{
int node, dist, cost;
Data(int a, int b, int c){
node = a;
dist = b;
cost = c;
}
};
struct Comparator{
bool operator() (Data a, Data b) {
return !(a.cost < b.cost);
}
};
class Solution {
public:
vector<vector<int>> cost;
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
cost = vector<vector<int> >(n + 1, vector<int>(K + 10, INT_MAX));
vector<vector<int> > graph[n];
for (int i = 0; i < flights.size(); i++) {
int u = flights[i][0];
int v = flights[i][1];
graph[u].push_back({ v, flights[i][2] });
}
priority_queue<Data, vector<Data>, Comparator> q;
q.push(Data(src, 0, 0));
cost[src][0] = 0;
int ans = -1;
while (!q.empty()) {
Data temp = q.top();
int curr = temp.node;
q.pop();
int dist = temp.dist;
if (curr == dst)
return temp.cost;
dist++;
if (dist > K + 1)
continue;
for (int i = 0; i < graph[curr].size(); i++) {
int neighbour = graph[curr][i][0];
if (cost[neighbour][dist] > cost[curr][dist - 1] + graph[curr][i][1]) {
cost[neighbour][dist] = cost[curr][dist - 1] + graph[curr][i][1];
q.push(Data(neighbour, dist, cost[neighbour][dist]));
}
}
}
return -1;
}
};
main(){
Solution ob;
vector<vector<int>> v = {{0,1,100},{1,2,100},{0,2,500}};
cout << (ob.findCheapestPrice(3, v, 0, 2, 1));
}Input
3, {{0,1,100},{1,2,100},{0,2,500}}, 0, 2, 1Output
200
581 Views
