Data Structure
Networking
RDBMS
Operating System
Java
MS Excel
iOS
HTML
CSS
Android
Python
C Programming
C++
C#
MongoDB
MySQL
Javascript
PHP
Physics
Chemistry
Biology
Mathematics
English
Economics
Psychology
Social Studies
Fashion Studies
Legal Studies
- Selected Reading
- UPSC IAS Exams Notes
- Developer's Best Practices
- Questions and Answers
- Effective Resume Writing
- HR Interview Questions
- Computer Glossary
- Who is Who
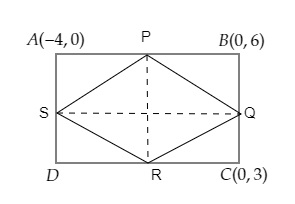
$ABCD$ is a rectangle formed by the points $A(-1, -1), B(-1, 4), C(5, 4)$ and $D(5, -1), P, Q, R$ and $S$ are the mid-points of $AB, BC, CD$ and $DA$ respectively. Is the quadrilateral $PQRS$ a square? a rectangle? or a rhombus? Justify your answer.
Given:
$ABCD$ is a rectangle formed by joining the points $A (-1, -1), B (-1, 4), C (5, 4)$ and $D (5, -1). P, Q, R$ and $S$ are the mid-points of sides $AB, BC, CD$ and $DA$ respectively.
To do:
We have to determine whether $PQRS$ is a square or a rectangle or a rhombus.
Solution:
Join $PR$ and $QS$. Let the point of intersection of $PR$ and QS$ be $O$.
Using the mid-point formula, we get,
The coordinates of $P$ are $(\frac{-2}{2}, \frac{3}{2})$
$=(-1, \frac{3}{2})$
Similarly,
The coordinates of $\mathrm{Q}$ are $(\frac{-1+5}{2}, \frac{4+4}{2})$
$=(\frac{4}{2}, \frac{8}{2})$
$=(2,4)$
The coordinates of $\mathrm{R}$ are $(\frac{5+5}{2}, \frac{4-1}{2})$
$=(\frac{10}{2}, \frac{3}{2})$
$=(5, \frac{3}{2})$
The coordinates of $\mathrm{S}$ are $(\frac{5-1}{2}, \frac{-1-1}{2})$
$=(\frac{4}{2}, \frac{-2}{2})$
$=(2,-1)$
Using distance formula, we get, $\mathrm{PQ}=\sqrt{(2+1)^{2}+(4-\frac{3} {2})^{2}}$
$=\sqrt{(3)^{2}+(\frac{5}{2})^{2}}$
$=\sqrt{9+\frac{25}{4}}$
$=\sqrt{\frac{36+25}{4}}$
$=\sqrt{\frac{61}{4}}$
$=\frac{\sqrt{61}}{2}$
$\mathrm{QR}=\sqrt{(5-2)^{2}+(\frac{3}{2}-4)^{2}}$ $=\sqrt{(3)^{2}+(\frac{-5}{2})^{2}}$
$=\sqrt{9+\frac{25}{4}}$
$=\sqrt{\frac{36+25}{4}}$
$=\sqrt{\frac{61}{4}}$
$=\frac{\sqrt{61}}{2}$
$O$ is the mid-point of $PR$. Coordinates of $\mathrm{O}$ are $(\frac{-1+5}{2}, \frac{\frac{3}{2}+\frac{3}{2}}{2})$
$=(\frac{4}{2}, \frac{3}{2})$
$=(2, \frac{3}{2})$
Similarly,
$\mathrm{O}$ is the mid-point of $\mathrm{QS}$,
Coordinates of $\mathrm{O}$ are $(\frac{2+2}{2}, \frac{4+(-1)}{2})$
$=(\frac{4}{2}, \frac{3}{2})$
$=(2, \frac{3}{2})$
We see that the coordinates of $\mathrm{O}$ in both the cases is same and adjacent sides are also equal.
This implies it may be a square or a rhombus.
$\mathrm{PR}=\sqrt{(5+1)^{2}+(\frac{3}{2}-\frac{3}{2})^{2}}$
$=\sqrt{(6)^{2}+(0)^{2}}$
$=\sqrt{36+0}$
$=\sqrt{36}$
$=6$
$\mathrm{QS}=\sqrt{(2-2)^{2}+(-1-4)^{2}}$
$=\sqrt{(0)^{2}+(-5)^{2}}$
$=\sqrt{0+25}$
$=\sqrt{25}$
$=5$
Here, diagonals are not equal.
Therefore, PQRS is a rhombus.
24 Views
