
- Signals and Systems Tutorial
- Signals & Systems Home
- Signals & Systems Overview
- Signals Basic Types
- Signals Classification
- Signals Basic Operations
- Systems Classification
- Signals Analysis
- Fourier Series
- Fourier Series Properties
- Fourier Series Types
- Fourier Transforms
- Fourier Transforms Properties
- Distortion Less Transmission
- Hilbert Transform
- Convolution and Correlation
- Signals Sampling Theorem
- Signals Sampling Techniques
- Laplace Transforms
- Laplace Transforms Properties
- Region of Convergence
- Z-Transforms (ZT)
- Z-Transforms Properties
- Signals and Systems Resources
- Signals and Systems - Resources
- Signals and Systems - Discussion
Signals Analysis
Analogy Between Vectors and Signals
There is a perfect analogy between vectors and signals.
Vector
A vector contains magnitude and direction. The name of the vector is denoted by bold face type and their magnitude is denoted by light face type.
Example: V is a vector with magnitude V. Consider two vectors V1 and V2 as shown in the following diagram. Let the component of V1 along with V2 is given by C12V2. The component of a vector V1 along with the vector V2 can obtained by taking a perpendicular from the end of V1 to the vector V2 as shown in diagram:
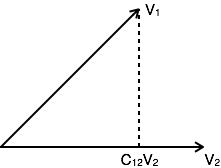
The vector V1 can be expressed in terms of vector V2
V1= C12V2 + Ve
Where Ve is the error vector.
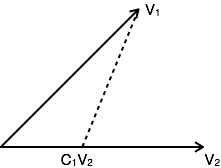
But this is not the only way of expressing vector V1 in terms of V2. The alternate possibilities are:
V1=C1V2+Ve1
V2=C2V2+Ve2
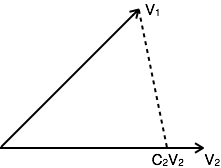
The error signal is minimum for large component value. If C12=0, then two signals are said to be orthogonal.
Dot Product of Two Vectors
V1 . V2 = V1.V2 cosθ
θ = Angle between V1 and V2
V1 . V2 =V2.V1
The components of V1 alogn V2 = V1 Cos θ = $V1.V2 \over V2$
From the diagram, components of V1 alogn V2 = C 12 V2
$$V_1.V_2 \over V_2 = C_12\,V_2$$
$$ \Rightarrow C_{12} = {V_1.V_2 \over V_2}$$
Signal
The concept of orthogonality can be applied to signals. Let us consider two signals f1(t) and f2(t). Similar to vectors, you can approximate f1(t) in terms of f2(t) as
f1(t) = C12 f2(t) + fe(t) for (t1 < t < t2)
$ \Rightarrow $ fe(t) = f1(t) – C12 f2(t)
One possible way of minimizing the error is integrating over the interval t1 to t2.
$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)] dt$$
$${1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_1(t) - C_{12}f_2(t)]dt $$
However, this step also does not reduce the error to appreciable extent. This can be corrected by taking the square of error function.
$\varepsilon = {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t)]^2 dt$
$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [f_e (t) - C_{12}f_2]^2 dt $
Where ε is the mean square value of error signal. The value of C12 which minimizes the error, you need to calculate ${d\varepsilon \over dC_{12} } = 0 $
$\Rightarrow {d \over dC_{12} } [ {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_1 (t) - C_{12} f_2 (t)]^2 dt]= 0 $
$\Rightarrow {1 \over {t_2 - t_1}} \int_{t_1}^{t_2} [ {d \over dC_{12} } f_{1}^2(t) - {d \over dC_{12} } 2f_1(t)C_{12}f_2(t)+ {d \over dC_{12} } f_{2}^{2} (t) C_{12}^2 ] dt =0 $
Derivative of the terms which do not have C12 term are zero.
$\Rightarrow \int_{t_1}^{t_2} - 2f_1(t) f_2(t) dt + 2C_{12}\int_{t_1}^{t_2}[f_{2}^{2} (t)]dt = 0 $
If $C_{12} = {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $ component is zero, then two signals are said to be orthogonal.
Put C12 = 0 to get condition for orthogonality.
0 = $ {{\int_{t_1}^{t_2}f_1(t)f_2(t)dt } \over {\int_{t_1}^{t_2} f_{2}^{2} (t)dt }} $
$$ \int_{t_1}^{t_2} f_1 (t)f_2(t) dt = 0 $$
Orthogonal Vector Space
A complete set of orthogonal vectors is referred to as orthogonal vector space. Consider a three dimensional vector space as shown below:

Consider a vector A at a point (X1, Y1, Z1). Consider three unit vectors (VX, VY, VZ) in the direction of X, Y, Z axis respectively. Since these unit vectors are mutually orthogonal, it satisfies that
$$V_X. V_X= V_Y. V_Y= V_Z. V_Z = 1 $$
$$V_X. V_Y= V_Y. V_Z= V_Z. V_X = 0 $$
You can write above conditions as
$$V_a . V_b = \left\{ \begin{array}{l l} 1 & \quad a = b \\ 0 & \quad a \neq b \end{array} \right. $$
The vector A can be represented in terms of its components and unit vectors as
$A = X_1 V_X + Y_1 V_Y + Z_1 V_Z................(1) $
Any vectors in this three dimensional space can be represented in terms of these three unit vectors only.
If you consider n dimensional space, then any vector A in that space can be represented as
$ A = X_1 V_X + Y_1 V_Y + Z_1 V_Z+...+ N_1V_N.....(2) $
As the magnitude of unit vectors is unity for any vector A
The component of A along x axis = A.VX
The component of A along Y axis = A.VY
The component of A along Z axis = A.VZ
Similarly, for n dimensional space, the component of A along some G axis
$= A.VG...............(3)$
Substitute equation 2 in equation 3.
$\Rightarrow CG= (X_1 V_X + Y_1 V_Y + Z_1 V_Z +...+G_1 V_G...+ N_1V_N)V_G$
$= X_1 V_X V_G + Y_1 V_Y V_G + Z_1 V_Z V_G +...+ G_1V_G V_G...+ N_1V_N V_G$
$= G_1 \,\,\,\,\, \text{since } V_G V_G=1$
$If V_G V_G \neq 1 \,\,\text{i.e.} V_G V_G= k$
$AV_G = G_1V_G V_G= G_1K$
$G_1 = {(AV_G) \over K}$
Orthogonal Signal Space
Let us consider a set of n mutually orthogonal functions x1(t), x2(t)... xn(t) over the interval t1 to t2. As these functions are orthogonal to each other, any two signals xj(t), xk(t) have to satisfy the orthogonality condition. i.e.
$$\int_{t_1}^{t_2} x_j(t)x_k(t)dt = 0 \,\,\, \text{where}\, j \neq k$$
$$\text{Let} \int_{t_1}^{t_2}x_{k}^{2}(t)dt = k_k $$
Let a function f(t), it can be approximated with this orthogonal signal space by adding the components along mutually orthogonal signals i.e.
$\,\,\,f(t) = C_1x_1(t) + C_2x_2(t) + ... + C_nx_n(t) + f_e(t) $
$\quad\quad=\Sigma_{r=1}^{n} C_rx_r (t) $
$\,\,\,f(t) = f(t) - \Sigma_{r=1}^n C_rx_r (t) $
Mean sqaure error $ \varepsilon = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f_e(t)]^2 dt$
$$ = {1 \over t_2 - t_2 } \int_{t_1}^{t_2} [ f[t] - \sum_{r=1}^{n} C_rx_r(t) ]^2 dt $$
The component which minimizes the mean square error can be found by
$$ {d\varepsilon \over dC_1} = {d\varepsilon \over dC_2} = ... = {d\varepsilon \over dC_k} = 0 $$
Let us consider ${d\varepsilon \over dC_k} = 0 $
$${d \over dC_k}[ {1 \over t_2 - t_1} \int_{t_1}^{t_2} [ f(t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt] = 0 $$
All terms that do not contain Ck is zero. i.e. in summation, r=k term remains and all other terms are zero.
$$\int_{t_1}^{t_2} - 2 f(t)x_k(t)dt + 2C_k \int_{t_1}^{t_2} [x_k^2 (t)] dt=0 $$
$$\Rightarrow C_k = {{\int_{t_1}^{t_2}f(t)x_k(t)dt} \over {int_{t_1}^{t_2} x_k^2 (t)dt}} $$
$$\Rightarrow \int_{t_1}^{t_2} f(t)x_k(t)dt = C_kK_k $$
Mean Square Error
The average of square of error function fe(t) is called as mean square error. It is denoted by ε (epsilon).
.$\varepsilon = {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t)]^2dt$
$\,\,\,\,= {1 \over t_2 - t_1 } \int_{t_1}^{t_2} [f_e (t) - \Sigma_{r=1}^n C_rx_r(t)]^2 dt $
$\,\,\,\,= {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f_e^2 (t) ]dt + \Sigma_{r=1}^{n} C_r^2 \int_{t_1}^{t_2} x_r^2 (t) dt - 2 \Sigma_{r=1}^{n} C_r \int_{t_1}^{t_2} x_r (t)f(t)dt$
You know that $C_{r}^{2} \int_{t_1}^{t_2} x_r^2 (t)dt = C_r \int_{t_1}^{t_2} x_r (t)f(d)dt = C_r^2 K_r $
$\varepsilon = {1 \over t_2 - t_1 } [ \int_{t_1}^{t_2} [f^2 (t)] dt + \Sigma_{r=1}^{n} C_r^2 K_r - 2 \Sigma_{r=1}^{n} C_r^2 K_r] $
$\,\,\,\,= {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt - \Sigma_{r=1}^{n} C_r^2 K_r ] $
$\, \therefore \varepsilon = {1 \over t_2 - t_1 } [\int_{t_1}^{t_2} [f^2 (t)] dt + (C_1^2 K_1 + C_2^2 K_2 + ... + C_n^2 K_n)] $
The above equation is used to evaluate the mean square error.
Closed and Complete Set of Orthogonal Functions
Let us consider a set of n mutually orthogonal functions x1(t), x2(t)...xn(t) over the interval t1 to t2. This is called as closed and complete set when there exist no function f(t) satisfying the condition $\int_{t_1}^{t_2} f(t)x_k(t)dt = 0 $
If this function is satisfying the equation $\int_{t_1}^{t_2} f(t)x_k(t)dt=0 \,\, \text{for}\, k = 1,2,..$ then f(t) is said to be orthogonal to each and every function of orthogonal set. This set is incomplete without f(t). It becomes closed and complete set when f(t) is included.
f(t) can be approximated with this orthogonal set by adding the components along mutually orthogonal signals i.e.
$$f(t) = C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t) + f_e(t) $$
If the infinite series $C_1 x_1(t) + C_2 x_2(t) + ... + C_n x_n(t)$ converges to f(t) then mean square error is zero.
Orthogonality in Complex Functions
If f1(t) and f2(t) are two complex functions, then f1(t) can be expressed in terms of f2(t) as
$f_1(t) = C_{12}f_2(t) \,\,\,\,\,\,\,\,$ ..with negligible error
Where $C_{12} = {{\int_{t_1}^{t_2} f_1(t)f_2^*(t)dt} \over { \int_{t_1}^{t_2} |f_2(t)|^2 dt}} $
Where $f_2^* (t)$ = complex conjugate of f2(t).
If f1(t) and f2(t) are orthogonal then C12 = 0
$$ {\int_{t_1}^{t_2} f_1 (t) f_2^*(t) dt \over \int_{t_1}^{t_2} |f_2 (t) |^2 dt} = 0 $$
$$\Rightarrow \int_{t_1}^{t_2} f_1 (t) f_2^* (dt) = 0$$
The above equation represents orthogonality condition in complex functions.
