
- Parallel Algorithm Tutorial
- Parallel Algorithm Home
- Parallel Algorithm Introduction
- Parallel Algorithm Analysis
- Parallel Algorithm Models
- Parallel Random Access Machines
- Parallel Algorithm Structure
- Design Techniques
- Matrix Multiplication
- Parallel Algorithm - Sorting
- Parallel Search Algorithm
- Graph Algorithm
- Parallel Algorithm Useful Resources
- Parallel Algorithm - Quick Guide
- Parallel Algorithm - Useful Resources
- Parallel Algorithm - Discussion
Parallel Algorithm - Sorting
Sorting is a process of arranging elements in a group in a particular order, i.e., ascending order, descending order, alphabetic order, etc. Here we will discuss the following −
- Enumeration Sort
- Odd-Even Transposition Sort
- Parallel Merge Sort
- Hyper Quick Sort
Sorting a list of elements is a very common operation. A sequential sorting algorithm may not be efficient enough when we have to sort a huge volume of data. Therefore, parallel algorithms are used in sorting.
Enumeration Sort
Enumeration sort is a method of arranging all the elements in a list by finding the final position of each element in a sorted list. It is done by comparing each element with all other elements and finding the number of elements having smaller value.
Therefore, for any two elements, ai and aj any one of the following cases must be true −
- ai < aj
- ai > aj
- ai = aj
Algorithm
procedure ENUM_SORTING (n)
begin
for each process P1,j do
C[j] := 0;
for each process Pi, j do
if (A[i] < A[j]) or A[i] = A[j] and i < j) then
C[j] := 1;
else
C[j] := 0;
for each process P1, j do
A[C[j]] := A[j];
end ENUM_SORTING
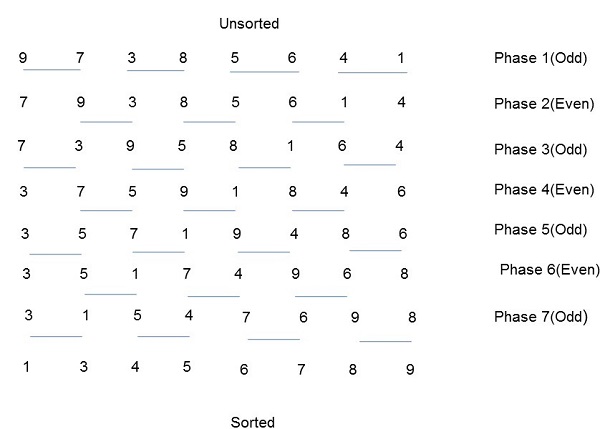
Odd-Even Transposition Sort
Odd-Even Transposition Sort is based on the Bubble Sort technique. It compares two adjacent numbers and switches them, if the first number is greater than the second number to get an ascending order list. The opposite case applies for a descending order series. Odd-Even transposition sort operates in two phases − odd phase and even phase. In both the phases, processes exchange numbers with their adjacent number in the right.
Algorithm
procedure ODD-EVEN_PAR (n)
begin
id := process's label
for i := 1 to n do
begin
if i is odd and id is odd then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
if i is even and id is even then
compare-exchange_min(id + 1);
else
compare-exchange_max(id - 1);
end for
end ODD-EVEN_PAR
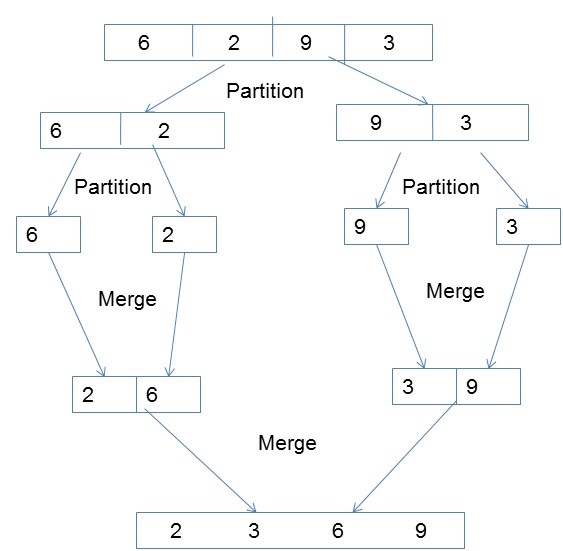
Parallel Merge Sort
Merge sort first divides the unsorted list into smallest possible sub-lists, compares it with the adjacent list, and merges it in a sorted order. It implements parallelism very nicely by following the divide and conquer algorithm.
Algorithm
procedureparallelmergesort(id, n, data, newdata)
begin
data = sequentialmergesort(data)
for dim = 1 to n
data = parallelmerge(id, dim, data)
endfor
newdata = data
end
Hyper Quick Sort
Hyper quick sort is an implementation of quick sort on hypercube. Its steps are as follows −
- Divide the unsorted list among each node.
- Sort each node locally.
- From node 0, broadcast the median value.
- Split each list locally, then exchange the halves across the highest dimension.
- Repeat steps 3 and 4 in parallel until the dimension reaches 0.
Algorithm
procedure HYPERQUICKSORT (B, n)
begin
id := process’s label;
for i := 1 to d do
begin
x := pivot;
partition B into B1 and B2 such that B1 ≤ x < B2;
if ith bit is 0 then
begin
send B2 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B1 U C;
endif
else
send B1 to the process along the ith communication link;
C := subsequence received along the ith communication link;
B := B2 U C;
end else
end for
sort B using sequential quicksort;
end HYPERQUICKSORT