Computer Graphics - Quick Guide

Computer Graphics - Basics

Computer graphics is an art of drawing pictures on computer screens with the help of programming. It involves computations, creation, and manipulation of data. In other words, we can say that computer graphics is a rendering tool for the generation and manipulation of images.

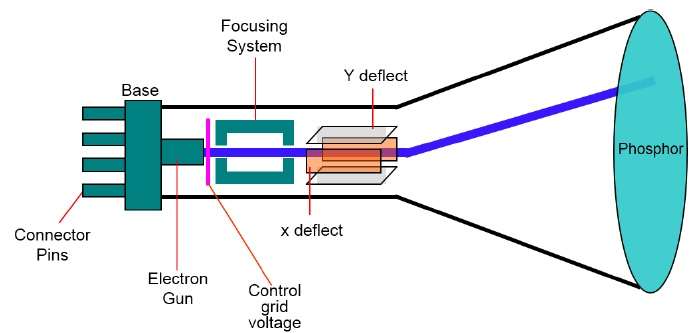
Cathode Ray Tube

The primary output device in a graphical system is the video monitor. The main element of a video monitor is the Cathode Ray Tube (CRT), shown in the following illustration.

The operation of CRT is very simple −

The electron gun emits a beam of electrons (cathode rays).
The electron beam passes through focusing and deflection systems that direct it towards specified positions on the phosphor-coated screen.
When the beam hits the screen, the phosphor emits a small spot of light at each position contacted by the electron beam.
It redraws the picture by directing the electron beam back over the same screen points quickly.

There are two ways (Random scan and Raster scan) by which we can display an object on the screen.

Raster Scan

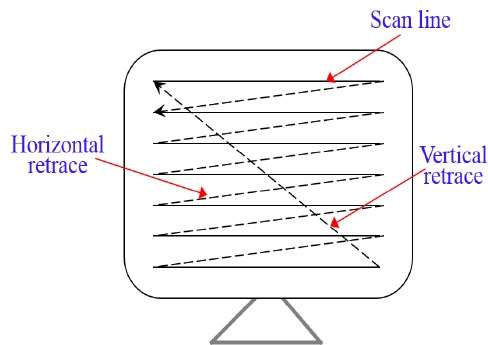
In a raster scan system, the electron beam is swept across the screen, one row at a time from top to bottom. As the electron beam moves across each row, the beam intensity is turned on and off to create a pattern of illuminated spots.

Picture definition is stored in memory area called the Refresh Buffer or Frame Buffer. This memory area holds the set of intensity values for all the screen points. Stored intensity values are then retrieved from the refresh buffer and “painted” on the screen one row (scan line) at a time as shown in the following illustration.

Each screen point is referred to as a pixel (picture element) or pel. At the end of each scan line, the electron beam returns to the left side of the screen to begin displaying the next scan line.

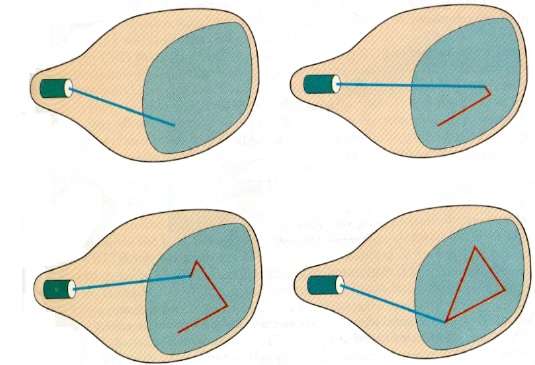
Random Scan (Vector Scan)

In this technique, the electron beam is directed only to the part of the screen where the picture is to be drawn rather than scanning from left to right and top to bottom as in raster scan. It is also called vector display, stroke-writing display, or calligraphic display.

Picture definition is stored as a set of line-drawing commands in an area of memory referred to as the refresh display file. To display a specified picture, the system cycles through the set of commands in the display file, drawing each component line in turn. After all the line-drawing commands are processed, the system cycles back to the first line command in the list.

Random-scan displays are designed to draw all the component lines of a picture 30 to 60 times each second.

Application of Computer Graphics

Computer Graphics has numerous applications, some of which are listed below −

Computer graphics user interfaces (GUIs) − A graphic, mouse-oriented paradigm which allows the user to interact with a computer.
Business presentation graphics − "A picture is worth a thousand words".
Cartography − Drawing maps.
Weather Maps − Real-time mapping, symbolic representations.
Satellite Imaging − Geodesic images.
Photo Enhancement − Sharpening blurred photos.
Medical imaging − MRIs, CAT scans, etc. - Non-invasive internal examination.
Engineering drawings − mechanical, electrical, civil, etc. - Replacing the blueprints of the past.
Typography − The use of character images in publishing - replacing the hard type of the past.
Architecture − Construction plans, exterior sketches - replacing the blueprints and hand drawings of the past.
Art − Computers provide a new medium for artists.
Training − Flight simulators, computer aided instruction, etc.
Entertainment − Movies and games.
Simulation and modeling − Replacing physical modeling and enactments

Line Generation Algorithm

A line connects two points. It is a basic element in graphics. To draw a line, you need two points between which you can draw a line. In the following three algorithms, we refer the one point of line as $X_{0}, Y_{0}$ and the second point of line as $X_{1}, Y_{1}$.

DDA Algorithm

Digital Differential Analyzer (DDA) algorithm is the simple line generation algorithm which is explained step by step here.

Step 1 − Get the input of two end points $(X_{0}, Y_{0})$ and $(X_{1}, Y_{1})$.

Step 2 − Calculate the difference between two end points.

dx = X₁ - X₀
dy = Y₁ - Y₀

Step 3 − Based on the calculated difference in step-2, you need to identify the number of steps to put pixel. If dx > dy, then you need more steps in x coordinate; otherwise in y coordinate.

if (absolute(dx) > absolute(dy))
   Steps = absolute(dx);
else
   Steps = absolute(dy);

Step 4 − Calculate the increment in x coordinate and y coordinate.

Xincrement = dx / (float) steps;
Yincrement = dy / (float) steps;

Step 5 − Put the pixel by successfully incrementing x and y coordinates accordingly and complete the drawing of the line.

for(int v=0; v < Steps; v++)
{
   x = x + Xincrement;
   y = y + Yincrement;
   putpixel(Round(x), Round(y));
}

Bresenham’s Line Generation

The Bresenham algorithm is another incremental scan conversion algorithm. The big advantage of this algorithm is that, it uses only integer calculations. Moving across the x axis in unit intervals and at each step choose between two different y coordinates.

For example, as shown in the following illustration, from position (2, 3) you need to choose between (3, 3) and (3, 4). You would like the point that is closer to the original line.

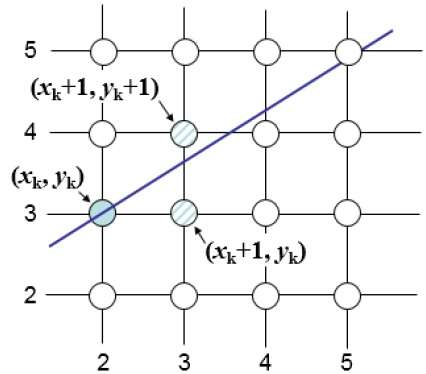
At sample position $X_{k}+1,$ the vertical separations from the mathematical line are labelled as $d_{upper}$ and $d_{lower}$.

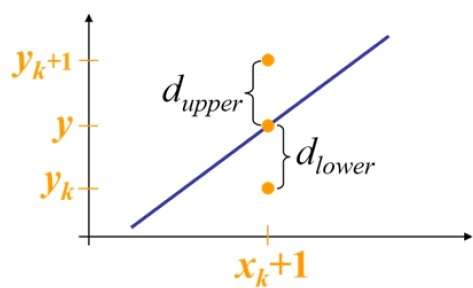
From the above illustration, the y coordinate on the mathematical line at $x_{k}+1$ is −

Y = m($X_{k}$+1) + b

So, $d_{upper}$ and $d_{lower}$ are given as follows −

$$d_{lower} = y-y_{k}$$

$$= m(X_{k} + 1) + b - Y_{k}$$

and

$$d_{upper} = (y_{k} + 1) - y$$

$= Y_{k} + 1 - m (X_{k} + 1) - b$

You can use these to make a simple decision about which pixel is closer to the mathematical line. This simple decision is based on the difference between the two pixel positions.

$$d_{lower} - d_{upper} = 2m(x_{k} + 1) - 2y_{k} + 2b - 1$$

Let us substitute m with dy/dx where dx and dy are the differences between the end-points.

$$dx (d_{lower} - d_{upper}) =dx(2\frac{\mathrm{d} y}{\mathrm{d} x}(x_{k} + 1) - 2y_{k} + 2b - 1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + 2dy + 2dx(2b-1)$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

So, a decision parameter $P_{k}$ for the kth step along a line is given by −

$$p_{k} = dx(d_{lower} - d_{upper})$$

$$ = 2dy.x_{k} - 2dx.y_{k} + C$$

The sign of the decision parameter $P_{k}$ is the same as that of $d_{lower} - d_{upper}$.

If $p_{k}$ is negative, then choose the lower pixel, otherwise choose the upper pixel.

Remember, the coordinate changes occur along the x axis in unit steps, so you can do everything with integer calculations. At step k+1, the decision parameter is given as −

$$p_{k +1} = 2dy.x_{k + 1} - 2dx.y_{k + 1} + C$$

Subtracting $p_{k}$ from this we get −

$$p_{k + 1} - p_{k} = 2dy(x_{k + 1} - x_{k}) - 2dx(y_{k + 1} - y_{k})$$

But, $x_{k+1}$ is the same as $x_{k+1}$. So −

$$p_{k+1} = p_{k} + 2dy - 2dx(y_{k+1} - y_{k})$$

Where, $Y_{k+1} – Y_{k}$ is either 0 or 1 depending on the sign of $P_{k}$.

The first decision parameter $p_{0}$ is evaluated at $(x_{0}, y_{0})$ is given as −

$$p_{0} = 2dy - dx$$

Now, keeping in mind all the above points and calculations, here is the Bresenham algorithm for slope m < 1 −

Step 1 − Input the two end-points of line, storing the left end-point in $(x_{0}, y_{0})$.

Step 2 − Plot the point $(x_{0}, y_{0})$.

Step 3 − Calculate the constants dx, dy, 2dy, and (2dy – 2dx) and get the first value for the decision parameter as −

$$p_{0} = 2dy - dx$$

Step 4 − At each $X_{k}$ along the line, starting at k = 0, perform the following test −

If $p_{k}$ < 0, the next point to plot is $(x_{k}+1, y_{k})$ and

$$p_{k+1} = p_{k} + 2dy$$ Otherwise,

$$(x_{k}, y_{k}+1)$$

$$p_{k+1} = p_{k} + 2dy - 2dx$$

Step 5 − Repeat step 4 (dx – 1) times.

For m > 1, find out whether you need to increment x while incrementing y each time.

After solving, the equation for decision parameter $P_{k}$ will be very similar, just the x and y in the equation gets interchanged.

Mid-Point Algorithm

Mid-point algorithm is due to Bresenham which was modified by Pitteway and Van Aken. Assume that you have already put the point P at (x, y) coordinate and the slope of the line is 0 ≤ k ≤ 1 as shown in the following illustration.

Now you need to decide whether to put the next point at E or N. This can be chosen by identifying the intersection point Q closest to the point N or E. If the intersection point Q is closest to the point N then N is considered as the next point; otherwise E.

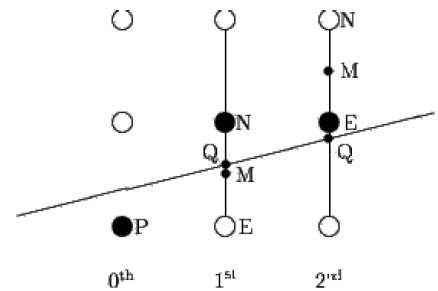
To determine that, first calculate the mid-point M(x+1, y + ½). If the intersection point Q of the line with the vertical line connecting E and N is below M, then take E as the next point; otherwise take N as the next point.

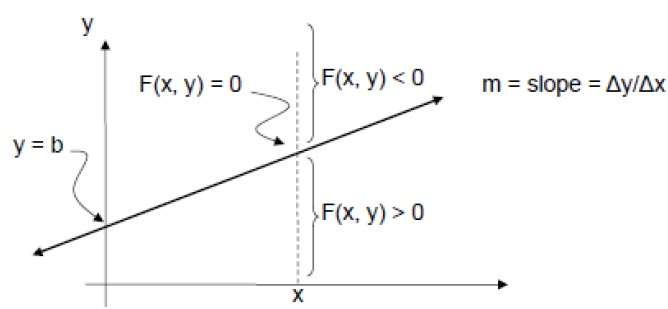
In order to check this, we need to consider the implicit equation −

F(x,y) = mx + b - y

For positive m at any given X,

If y is on the line, then F(x, y) = 0
If y is above the line, then F(x, y) < 0
If y is below the line, then F(x, y) > 0

Circle Generation Algorithm

Drawing a circle on the screen is a little complex than drawing a line. There are two popular algorithms for generating a circle − Bresenham’s Algorithm and Midpoint Circle Algorithm. These algorithms are based on the idea of determining the subsequent points required to draw the circle. Let us discuss the algorithms in detail −

The equation of circle is $X^{2} + Y^{2} = r^{2},$ where r is radius.

Bresenham’s Algorithm

We cannot display a continuous arc on the raster display. Instead, we have to choose the nearest pixel position to complete the arc.

From the following illustration, you can see that we have put the pixel at (X, Y) location and now need to decide where to put the next pixel − at N (X+1, Y) or at S (X+1, Y-1).

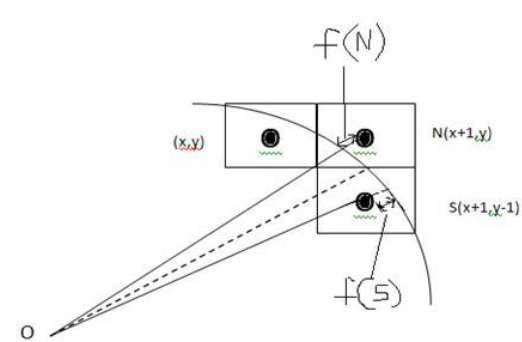
This can be decided by the decision parameter d.

If d <= 0, then N(X+1, Y) is to be chosen as next pixel.
If d > 0, then S(X+1, Y-1) is to be chosen as the next pixel.

Algorithm

Step 1 − Get the coordinates of the center of the circle and radius, and store them in x, y, and R respectively. Set P=0 and Q=R.

Step 2 − Set decision parameter D = 3 – 2R.

Step 3 − Repeat through step-8 while P ≤ Q.

Step 4 − Call Draw Circle (X, Y, P, Q).

Step 5 − Increment the value of P.

Step 6 − If D < 0 then D = D + 4P + 6.

Step 7 − Else Set R = R - 1, D = D + 4(P-Q) + 10.

Step 8 − Call Draw Circle (X, Y, P, Q).

Draw Circle Method(X, Y, P, Q).

Call Putpixel (X + P, Y + Q).
Call Putpixel (X - P, Y + Q).
Call Putpixel (X + P, Y - Q).
Call Putpixel (X - P, Y - Q).
Call Putpixel (X + Q, Y + P).
Call Putpixel (X - Q, Y + P).
Call Putpixel (X + Q, Y - P).
Call Putpixel (X - Q, Y - P).

Mid Point Algorithm

Step 1 − Input radius r and circle center $(x_{c,} y_{c})$ and obtain the first point on the circumference of the circle centered on the origin as

(x₀, y₀) = (0, r)

Step 2 − Calculate the initial value of decision parameter as

$P_{0}$ = 5/4 – r (See the following description for simplification of this equation.)

f(x, y) = x² + y² - r² = 0

f(x_i - 1/2 + e, y_i + 1)
        = (x_i - 1/2 + e)² + (y_i + 1)² - r² 
        = (x_i- 1/2)² + (y_i + 1)² - r² + 2(x_i - 1/2)e + e²
        = f(x_i - 1/2, y_i + 1) + 2(x_i - 1/2)e + e² = 0

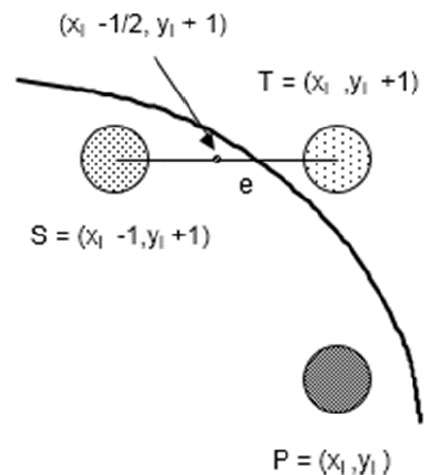
Let d_i = f(x_i - 1/2, y_i + 1) = -2(x_i - 1/2)e - e²
Thus,

If e < 0 then di > 0 so choose point S = (x_i - 1, y_i + 1).
d_i+1    = f(x_i - 1 - 1/2, y_i + 1 + 1) = ((x_i - 1/2) - 1)² + ((y_i + 1) + 1)² - r²
        = d_i - 2(x_i - 1) + 2(y_i + 1) + 1
        = d_i + 2(y_{i + 1} - x_{i + 1}) + 1
		  
If e >= 0 then di <= 0 so choose point T = (x_i, y_i + 1)
   d_i+1 = f(x_i - 1/2, y_i + 1 + 1)
       = d_i + 2y_i+1 + 1
		  
The initial value of di is
   d₀ = f(r - 1/2, 0 + 1) = (r - 1/2)² + 1² - r²
      = 5/4 - r {1-r can be used if r is an integer}
		
When point S = (x_i - 1, y_i + 1) is chosen then
   d_i+1 = d_i + -2x_i+1 + 2y_i+1 + 1
	
When point T = (x_i, y_i + 1) is chosen then
   d_i+1 = d_i + 2y_i+1 + 1

Step 3 − At each $X_{K}$ position starting at K=0, perform the following test −

If P_K < 0 then next point on circle (0,0) is (X_K+1,Y_K) and
   P_K+1 = P_K + 2X_K+1 + 1
Else
   P_K+1 = P_K + 2X_K+1 + 1 – 2Y_K+1
	
Where, 2X_K+1 = 2X_K+2 and 2Y_K+1 = 2Y_K-2.

Step 4 − Determine the symmetry points in other seven octants.

Step 5 − Move each calculate pixel position (X, Y) onto the circular path centered on $(X_{C,} Y_{C})$ and plot the coordinate values.

X = X + X_C,   Y = Y + Y_C

Step 6 − Repeat step-3 through 5 until X >= Y.

Polygon Filling Algorithm

Polygon is an ordered list of vertices as shown in the following figure. For filling polygons with particular colors, you need to determine the pixels falling on the border of the polygon and those which fall inside the polygon. In this chapter, we will see how we can fill polygons using different techniques.

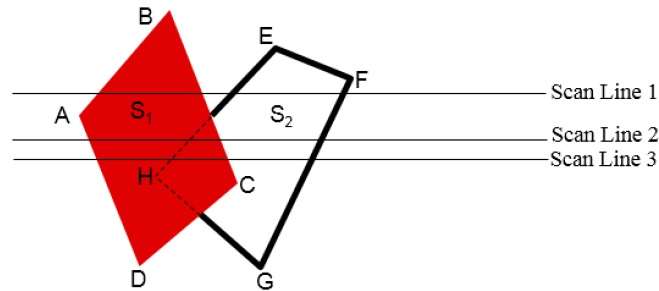
Scan Line Algorithm

This algorithm works by intersecting scanline with polygon edges and fills the polygon between pairs of intersections. The following steps depict how this algorithm works.

Step 1 − Find out the Ymin and Ymax from the given polygon.

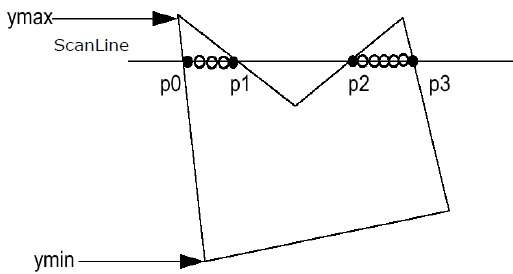
Step 2 − ScanLine intersects with each edge of the polygon from Ymin to Ymax. Name each intersection point of the polygon. As per the figure shown above, they are named as p0, p1, p2, p3.

Step 3 − Sort the intersection point in the increasing order of X coordinate i.e. (p0, p1), (p1, p2), and (p2, p3).

Step 4 − Fill all those pair of coordinates that are inside polygons and ignore the alternate pairs.

Flood Fill Algorithm

Sometimes we come across an object where we want to fill the area and its boundary with different colors. We can paint such objects with a specified interior color instead of searching for particular boundary color as in boundary filling algorithm.

Instead of relying on the boundary of the object, it relies on the fill color. In other words, it replaces the interior color of the object with the fill color. When no more pixels of the original interior color exist, the algorithm is completed.

Once again, this algorithm relies on the Four-connect or Eight-connect method of filling in the pixels. But instead of looking for the boundary color, it is looking for all adjacent pixels that are a part of the interior.

Boundary Fill Algorithm

The boundary fill algorithm works as its name. This algorithm picks a point inside an object and starts to fill until it hits the boundary of the object. The color of the boundary and the color that we fill should be different for this algorithm to work.

In this algorithm, we assume that color of the boundary is same for the entire object. The boundary fill algorithm can be implemented by 4-connected pixels or 8-connected pixels.

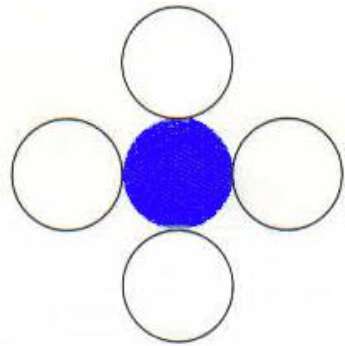
4-Connected Polygon

In this technique 4-connected pixels are used as shown in the figure. We are putting the pixels above, below, to the right, and to the left side of the current pixels and this process will continue until we find a boundary with different color.

Algorithm

Step 1 − Initialize the value of seed point (seedx, seedy), fcolor and dcol.

Step 2 − Define the boundary values of the polygon.

Step 3 − Check if the current seed point is of default color, then repeat the steps 4 and 5 till the boundary pixels reached.

If getpixel(x, y) = dcol then repeat step 4 and 5

Step 4 − Change the default color with the fill color at the seed point.

setPixel(seedx, seedy, fcol)

Step 5 − Recursively follow the procedure with four neighborhood points.

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)

Step 6 − Exit

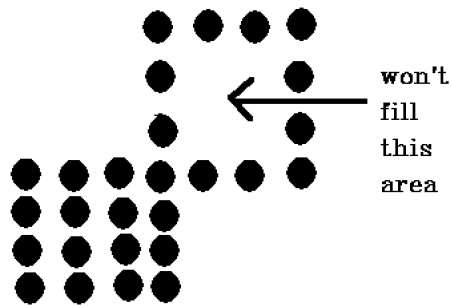
There is a problem with this technique. Consider the case as shown below where we tried to fill the entire region. Here, the image is filled only partially. In such cases, 4-connected pixels technique cannot be used.

8-Connected Polygon

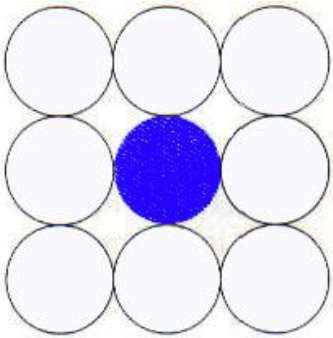
In this technique 8-connected pixels are used as shown in the figure. We are putting pixels above, below, right and left side of the current pixels as we were doing in 4-connected technique.

In addition to this, we are also putting pixels in diagonals so that entire area of the current pixel is covered. This process will continue until we find a boundary with different color.

Algorithm

Step 1 − Initialize the value of seed point (seedx, seedy), fcolor and dcol.

Step 2 − Define the boundary values of the polygon.

Step 3 − Check if the current seed point is of default color then repeat the steps 4 and 5 till the boundary pixels reached

If getpixel(x,y) = dcol then repeat step 4 and 5

Step 4 − Change the default color with the fill color at the seed point.

setPixel(seedx, seedy, fcol)

Step 5 − Recursively follow the procedure with four neighbourhood points

FloodFill (seedx – 1, seedy, fcol, dcol)
FloodFill (seedx + 1, seedy, fcol, dcol)
FloodFill (seedx, seedy - 1, fcol, dcol)
FloodFill (seedx, seedy + 1, fcol, dcol)
FloodFill (seedx – 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy + 1, fcol, dcol)
FloodFill (seedx + 1, seedy - 1, fcol, dcol)
FloodFill (seedx – 1, seedy - 1, fcol, dcol)

Step 6 − Exit

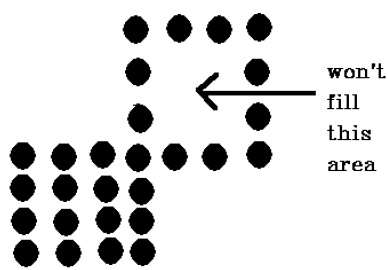
The 4-connected pixel technique failed to fill the area as marked in the following figure which won’t happen with the 8-connected technique.

Inside-outside Test

This method is also known as counting number method. While filling an object, we often need to identify whether particular point is inside the object or outside it. There are two methods by which we can identify whether particular point is inside an object or outside.

Odd-Even Rule
Nonzero winding number rule

Odd-Even Rule

In this technique, we count the edge crossing along the line from any point (x, y) to infinity. If the number of interactions is odd then the point (x, y) is an interior point. If the number of interactions is even then point (x, y) is an exterior point. Here is the example to give you the clear idea −

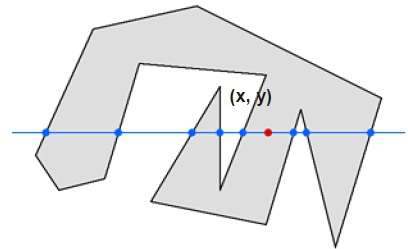
From the above figure, we can see that from the point (x, y), the number of interactions point on the left side is 5 and on the right side is 3. So the total number of interaction point is 8, which is odd. Hence, the point is considered within the object.

Nonzero Winding Number Rule

This method is also used with the simple polygons to test the given point is interior or not. It can be simply understood with the help of a pin and a rubber band. Fix up the pin on one of the edge of the polygon and tie-up the rubber band in it and then stretch the rubber band along the edges of the polygon.

When all the edges of the polygon are covered by the rubber band, check out the pin which has been fixed up at the point to be test. If we find at least one wind at the point consider it within the polygon, else we can say that the point is not inside the polygon.

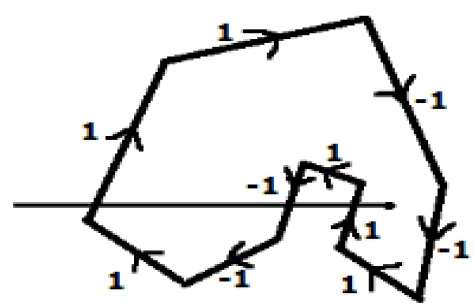
In another alternative method, give directions to all the edges of the polygon. Draw a scan line from the point to be test towards the left most of X direction.

Give the value 1 to all the edges which are going to upward direction and all other -1 as direction values.
Check the edge direction values from which the scan line is passing and sum up them.
If the total sum of this direction value is non-zero, then this point to be tested is an interior point, otherwise it is an exterior point.
In the above figure, we sum up the direction values from which the scan line is passing then the total is 1 – 1 + 1 = 1; which is non-zero. So the point is said to be an interior point.

Viewing & Clipping

The primary use of clipping in computer graphics is to remove objects, lines, or line segments that are outside the viewing pane. The viewing transformation is insensitive to the position of points relative to the viewing volume − especially those points behind the viewer − and it is necessary to remove these points before generating the view.

Point Clipping

Clipping a point from a given window is very easy. Consider the following figure, where the rectangle indicates the window. Point clipping tells us whether the given point (X, Y) is within the given window or not; and decides whether we will use the minimum and maximum coordinates of the window.

The X-coordinate of the given point is inside the window, if X lies in between Wx1 ≤ X ≤ Wx2. Same way, Y coordinate of the given point is inside the window, if Y lies in between Wy1 ≤ Y ≤ Wy2.

Line Clipping

The concept of line clipping is same as point clipping. In line clipping, we will cut the portion of line which is outside of window and keep only the portion that is inside the window.

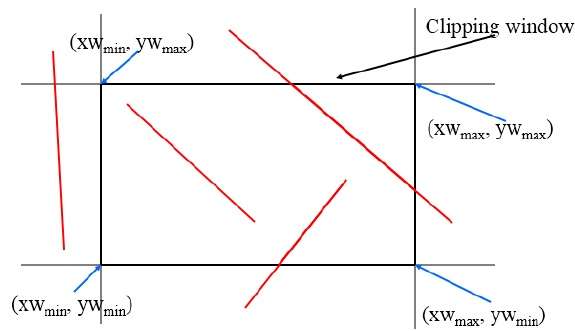
Cohen-Sutherland Line Clippings

This algorithm uses the clipping window as shown in the following figure. The minimum coordinate for the clipping region is $(XW_{min,} YW_{min})$ and the maximum coordinate for the clipping region is $(XW_{max,} YW_{max})$.

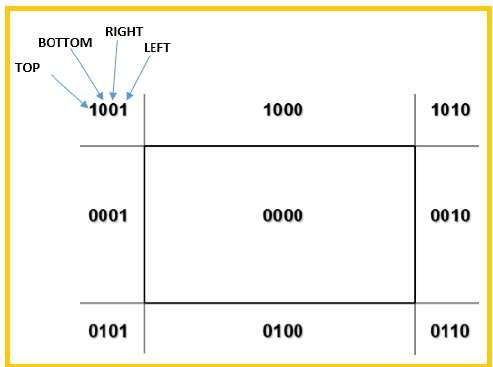
We will use 4-bits to divide the entire region. These 4 bits represent the Top, Bottom, Right, and Left of the region as shown in the following figure. Here, the TOP and LEFT bit is set to 1 because it is the TOP-LEFT corner.

There are 3 possibilities for the line −

Line can be completely inside the window (This line should be accepted).
Line can be completely outside of the window (This line will be completely removed from the region).
Line can be partially inside the window (We will find intersection point and draw only that portion of line that is inside region).

Algorithm

Step 1 − Assign a region code for each endpoints.

Step 2 − If both endpoints have a region code 0000 then accept this line.

Step 3 − Else, perform the logical ANDoperation for both region codes.

Step 3.1 − If the result is not 0000, then reject the line.

Step 3.2 − Else you need clipping.

Step 3.2.1 − Choose an endpoint of the line that is outside the window.

Step 3.2.2 − Find the intersection point at the window boundary (base on region code).

Step 3.2.3 − Replace endpoint with the intersection point and update the region code.

Step 3.2.4 − Repeat step 2 until we find a clipped line either trivially accepted or trivially rejected.

Step 4 − Repeat step 1 for other lines.

Cyrus-Beck Line Clipping Algorithm

This algorithm is more efficient than Cohen-Sutherland algorithm. It employs parametric line representation and simple dot products.

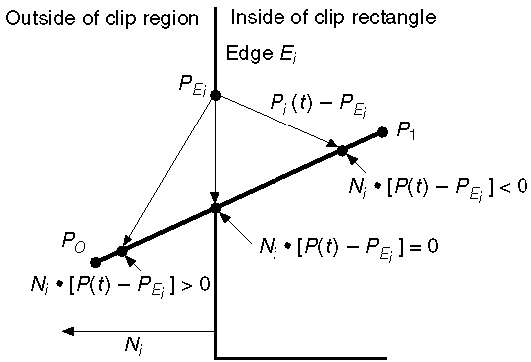
Parametric equation of line is −

P₀P₁:P(t) = P₀ + t(P₁-P₀)

Let N_i be the outward normal edge E_i. Now pick any arbitrary point P_Ei on edge E_i then the dot product N_i∙[P(t) – P_Ei] determines whether the point P(t) is “inside the clip edge” or “outside” the clip edge or “on” the clip edge.

The point P(t) is inside if N_i.[P(t) – P_Ei] < 0

The point P(t) is outside if N_i.[P(t) – P_Ei] > 0

The point P(t) is on the edge if N_i.[P(t) – P_Ei] = 0 (Intersection point)

N_i.[P(t) – P_Ei] = 0

N_i.[ P₀ + t(P₁-P₀) – P_Ei] = 0 (Replacing P(t) with P₀ + t(P₁-P₀))

N_i.[P₀ – P_Ei] + N_i.t[P₁-P₀] = 0

N_i.[P₀ – P_Ei] + N_i∙tD = 0 (substituting D for [P₁-P₀])

N_i.[P₀ – P_Ei] = - N_i∙tD

The equation for t becomes,

$$t = \tfrac{N_{i}.[P_{o} - P_{Ei}]}{{- N_{i}.D}}$$

It is valid for the following conditions −

N_i ≠ 0 (error cannot happen)
D ≠ 0 (P₁ ≠ P₀)
N_i∙D ≠ 0 (P₀P₁ not parallel to E_i)

Polygon Clipping (Sutherland Hodgman Algorithm)

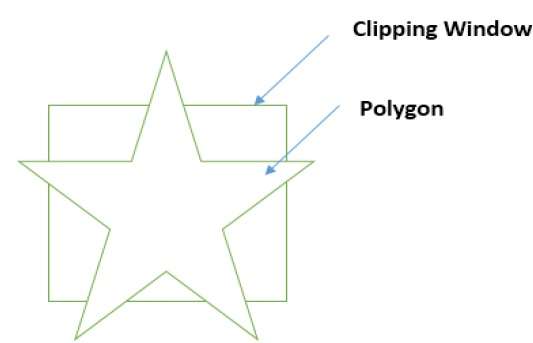
A polygon can also be clipped by specifying the clipping window. Sutherland Hodgeman polygon clipping algorithm is used for polygon clipping. In this algorithm, all the vertices of the polygon are clipped against each edge of the clipping window.

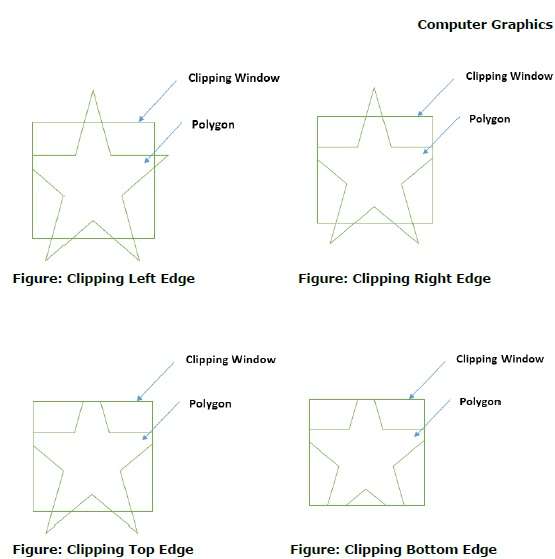
First the polygon is clipped against the left edge of the polygon window to get new vertices of the polygon. These new vertices are used to clip the polygon against right edge, top edge, bottom edge, of the clipping window as shown in the following figure.

While processing an edge of a polygon with clipping window, an intersection point is found if edge is not completely inside clipping window and the a partial edge from the intersection point to the outside edge is clipped. The following figures show left, right, top and bottom edge clippings −

Text Clipping

Various techniques are used to provide text clipping in a computer graphics. It depends on the methods used to generate characters and the requirements of a particular application. There are three methods for text clipping which are listed below −

All or none string clipping
All or none character clipping
Text clipping

The following figure shows all or none string clipping −

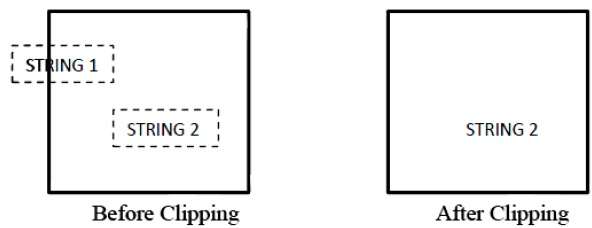
In all or none string clipping method, either we keep the entire string or we reject entire string based on the clipping window. As shown in the above figure, STRING2 is entirely inside the clipping window so we keep it and STRING1 being only partially inside the window, we reject.

The following figure shows all or none character clipping −

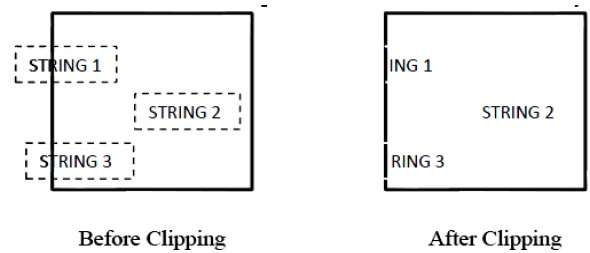
This clipping method is based on characters rather than entire string. In this method if the string is entirely inside the clipping window, then we keep it. If it is partially outside the window, then −

You reject only the portion of the string being outside
If the character is on the boundary of the clipping window, then we discard that entire character and keep the rest string.

The following figure shows text clipping −

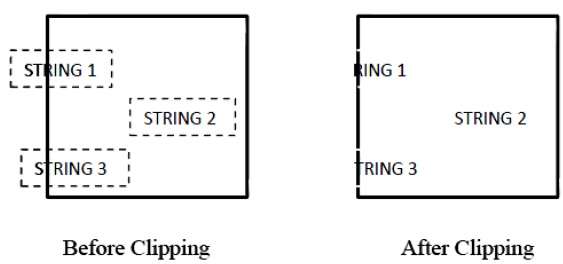
This clipping method is based on characters rather than the entire string. In this method if the string is entirely inside the clipping window, then we keep it. If it is partially outside the window, then

You reject only the portion of string being outside.
If the character is on the boundary of the clipping window, then we discard only that portion of character that is outside of the clipping window.

Bitmap Graphics

A bitmap is a collection of pixels that describes an image. It is a type of computer graphics that the computer uses to store and display pictures. In this type of graphics, images are stored bit by bit and hence it is named Bit-map graphics. For better understanding let us consider the following example where we draw a smiley face using bit-map graphics.

Now we will see how this smiley face is stored bit by bit in computer graphics.

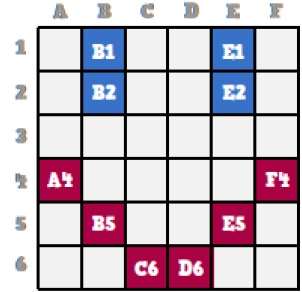
By observing the original smiley face closely, we can see that there are two blue lines which are represented as B1, B2 and E1, E2 in the above figure.

In the same way, the smiley is represented using the combination bits of A4, B5, C6, D6, E5, and F4 respectively.

The main disadvantages of bitmap graphics are −

We cannot resize the bitmap image. If you try to resize, the pixels get blurred.
Colored bitmaps can be very large.

2D Transformation

Transformation means changing some graphics into something else by applying rules. We can have various types of transformations such as translation, scaling up or down, rotation, shearing, etc. When a transformation takes place on a 2D plane, it is called 2D transformation.

Transformations play an important role in computer graphics to reposition the graphics on the screen and change their size or orientation.

Homogenous Coordinates

To perform a sequence of transformation such as translation followed by rotation and scaling, we need to follow a sequential process −

Translate the coordinates,
Rotate the translated coordinates, and then
Scale the rotated coordinates to complete the composite transformation.

To shorten this process, we have to use 3×3 transformation matrix instead of 2×2 transformation matrix. To convert a 2×2 matrix to 3×3 matrix, we have to add an extra dummy coordinate W.

In this way, we can represent the point by 3 numbers instead of 2 numbers, which is called Homogenous Coordinate system. In this system, we can represent all the transformation equations in matrix multiplication. Any Cartesian point P(X, Y) can be converted to homogenous coordinates by P’ (X_h, Y_h, h).

Translation

A translation moves an object to a different position on the screen. You can translate a point in 2D by adding translation coordinate (t_x, t_y) to the original coordinate (X, Y) to get the new coordinate (X’, Y’).

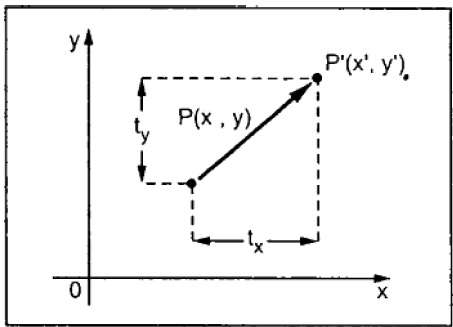
From the above figure, you can write that −

X’ = X + t_x

Y’ = Y + t_y

The pair (t_x, t_y) is called the translation vector or shift vector. The above equations can also be represented using the column vectors.

$P = \frac{[X]}{[Y]}$ p' = $\frac{[X']}{[Y']}$T = $\frac{[t_{x}]}{[t_{y}]}$

We can write it as −

P’ = P + T

Rotation

In rotation, we rotate the object at particular angle θ (theta) from its origin. From the following figure, we can see that the point P(X, Y) is located at angle φ from the horizontal X coordinate with distance r from the origin.

Let us suppose you want to rotate it at the angle θ. After rotating it to a new location, you will get a new point P’ (X’, Y’).

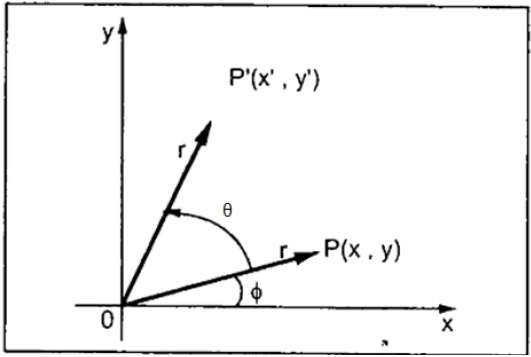
Using standard trigonometric the original coordinate of point P(X, Y) can be represented as −

$X = r \, cos \, \phi ...... (1)$

$Y = r \, sin \, \phi ...... (2)$

Same way we can represent the point P’ (X’, Y’) as −

${x}'= r \: cos \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: cos \: \theta \: − \: r \: sin \: \phi \: sin \: \theta ....... (3)$

${y}'= r \: sin \: \left ( \phi \: + \: \theta \right ) = r\: cos \: \phi \: sin \: \theta \: + \: r \: sin \: \phi \: cos \: \theta ....... (4)$

Substituting equation (1) & (2) in (3) & (4) respectively, we will get

${x}'= x \: cos \: \theta − \: y \: sin \: \theta $

${y}'= x \: sin \: \theta + \: y \: cos \: \theta $

Representing the above equation in matrix form,

$$[X' Y'] = [X Y] \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}OR $$

P’ = P ∙ R

Where R is the rotation matrix

$$R = \begin{bmatrix} cos\theta & sin\theta \\ −sin\theta & cos\theta \end{bmatrix}$$

The rotation angle can be positive and negative.

For positive rotation angle, we can use the above rotation matrix. However, for negative angle rotation, the matrix will change as shown below −

$$R = \begin{bmatrix} cos(−\theta) & sin(−\theta) \\ -sin(−\theta) & cos(−\theta) \end{bmatrix}$$

$$=\begin{bmatrix} cos\theta & −sin\theta \\ sin\theta & cos\theta \end{bmatrix} \left (\because cos(−\theta ) = cos \theta \; and\; sin(−\theta ) = −sin \theta \right )$$

Scaling

To change the size of an object, scaling transformation is used. In the scaling process, you either expand or compress the dimensions of the object. Scaling can be achieved by multiplying the original coordinates of the object with the scaling factor to get the desired result.

Let us assume that the original coordinates are (X, Y), the scaling factors are (S_X, S_Y), and the produced coordinates are (X’, Y’). This can be mathematically represented as shown below −

X' = X . S_X and Y' = Y . S_Y

The scaling factor S_X, S_Y scales the object in X and Y direction respectively. The above equations can also be represented in matrix form as below −

$$\binom{X'}{Y'} = \binom{X}{Y} \begin{bmatrix} S_{x} & 0\\ 0 & S_{y} \end{bmatrix}$$

P’ = P . S

Where S is the scaling matrix. The scaling process is shown in the following figure.

If we provide values less than 1 to the scaling factor S, then we can reduce the size of the object. If we provide values greater than 1, then we can increase the size of the object.

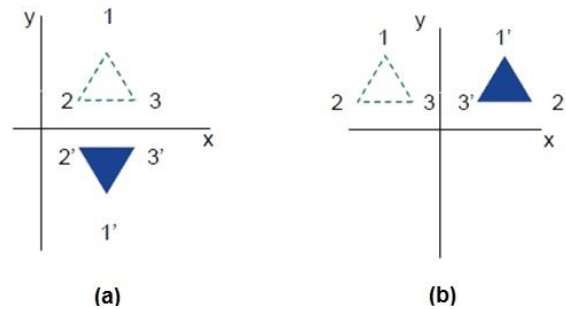
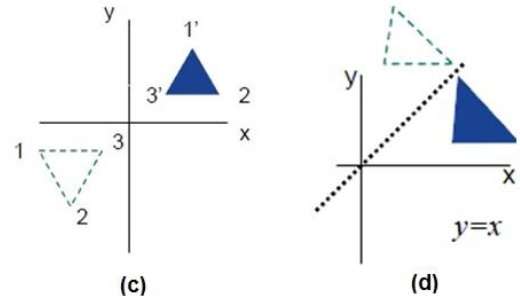
Reflection

Reflection is the mirror image of original object. In other words, we can say that it is a rotation operation with 180°. In reflection transformation, the size of the object does not change.

The following figures show reflections with respect to X and Y axes, and about the origin respectively.

Shear

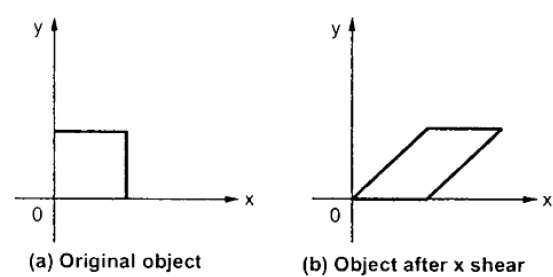
A transformation that slants the shape of an object is called the shear transformation. There are two shear transformations X-Shear and Y-Shear. One shifts X coordinates values and other shifts Y coordinate values. However; in both the cases only one coordinate changes its coordinates and other preserves its values. Shearing is also termed as Skewing.

X-Shear

The X-Shear preserves the Y coordinate and changes are made to X coordinates, which causes the vertical lines to tilt right or left as shown in below figure.

The transformation matrix for X-Shear can be represented as −

$$X_{sh} = \begin{bmatrix} 1& shx& 0\\ 0& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

Y' = Y + Sh_y . X

X’ = X

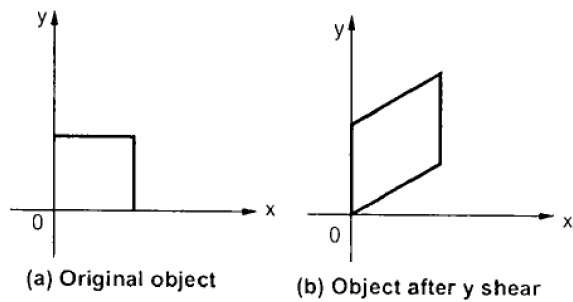
Y-Shear

The Y-Shear preserves the X coordinates and changes the Y coordinates which causes the horizontal lines to transform into lines which slopes up or down as shown in the following figure.

The Y-Shear can be represented in matrix from as −

$$Y_{sh} \begin{bmatrix} 1& 0& 0\\ shy& 1& 0\\ 0& 0& 1 \end{bmatrix}$$

X’ = X + Sh_x . Y

Y’ = Y

Composite Transformation

If a transformation of the plane T1 is followed by a second plane transformation T2, then the result itself may be represented by a single transformation T which is the composition of T1 and T2 taken in that order. This is written as T = T1∙T2.

Composite transformation can be achieved by concatenation of transformation matrices to obtain a combined transformation matrix.

A combined matrix −

[T][X] = [X] [T1] [T2] [T3] [T4] …. [Tn]

Where [Ti] is any combination of

Translation
Scaling
Shearing
Rotation
Reflection

The change in the order of transformation would lead to different results, as in general matrix multiplication is not cumulative, that is [A] . [B] ≠ [B] . [A] and the order of multiplication. The basic purpose of composing transformations is to gain efficiency by applying a single composed transformation to a point, rather than applying a series of transformation, one after another.

For example, to rotate an object about an arbitrary point (X_p, Y_p), we have to carry out three steps −

Translate point (X_p, Y_p) to the origin.
Rotate it about the origin.
Finally, translate the center of rotation back where it belonged.

3D Computer Graphics

In the 2D system, we use only two coordinates X and Y but in 3D, an extra coordinate Z is added. 3D graphics techniques and their application are fundamental to the entertainment, games, and computer-aided design industries. It is a continuing area of research in scientific visualization.

Furthermore, 3D graphics components are now a part of almost every personal computer and, although traditionally intended for graphics-intensive software such as games, they are increasingly being used by other applications.

Parallel Projection

Parallel projection discards z-coordinate and parallel lines from each vertex on the object are extended until they intersect the view plane. In parallel projection, we specify a direction of projection instead of center of projection.

In parallel projection, the distance from the center of projection to project plane is infinite. In this type of projection, we connect the projected vertices by line segments which correspond to connections on the original object.

Parallel projections are less realistic, but they are good for exact measurements. In this type of projections, parallel lines remain parallel and angles are not preserved. Various types of parallel projections are shown in the following hierarchy.

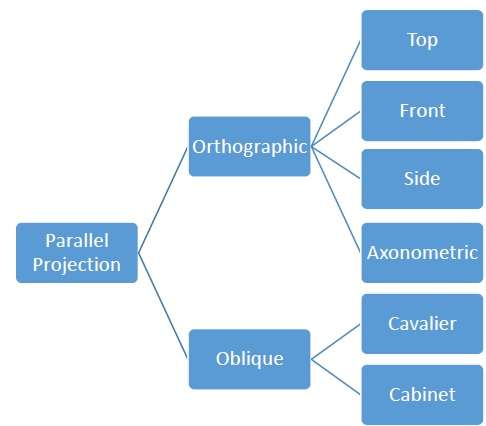
Orthographic Projection

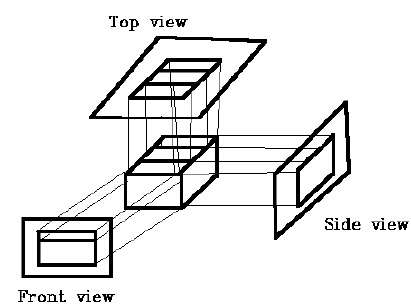
In orthographic projection the direction of projection is normal to the projection of the plane. There are three types of orthographic projections −

Front Projection
Top Projection
Side Projection

Oblique Projection

In oblique projection, the direction of projection is not normal to the projection of plane. In oblique projection, we can view the object better than orthographic projection.

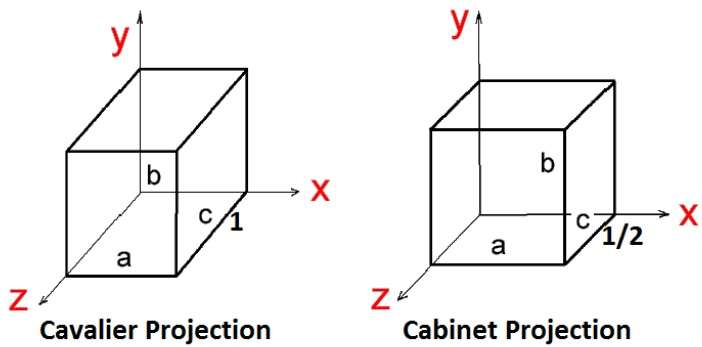
There are two types of oblique projections − Cavalier and Cabinet. The Cavalier projection makes 45° angle with the projection plane. The projection of a line perpendicular to the view plane has the same length as the line itself in Cavalier projection. In a cavalier projection, the foreshortening factors for all three principal directions are equal.

The Cabinet projection makes 63.4° angle with the projection plane. In Cabinet projection, lines perpendicular to the viewing surface are projected at ½ their actual length. Both the projections are shown in the following figure −

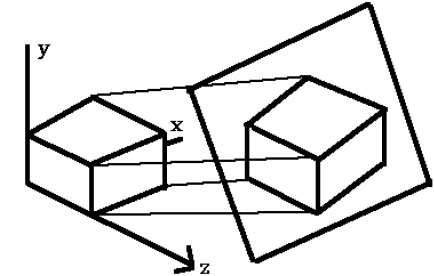
Isometric Projections

Orthographic projections that show more than one side of an object are called axonometric orthographic projections. The most common axonometric projection is an isometric projection where the projection plane intersects each coordinate axis in the model coordinate system at an equal distance. In this projection parallelism of lines are preserved but angles are not preserved. The following figure shows isometric projection −

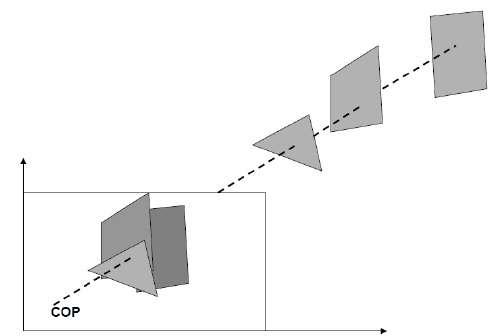
Perspective Projection

In perspective projection, the distance from the center of projection to project plane is finite and the size of the object varies inversely with distance which looks more realistic.

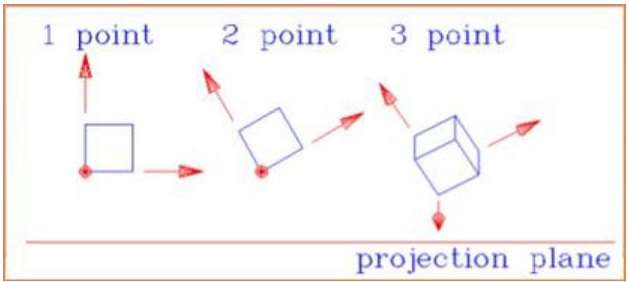
The distance and angles are not preserved and parallel lines do not remain parallel. Instead, they all converge at a single point called center of projection or projection reference point. There are 3 types of perspective projections which are shown in the following chart.

One point perspective projection is simple to draw.
Two point perspective projection gives better impression of depth.
Three point perspective projection is most difficult to draw.

The following figure shows all the three types of perspective projection −

Translation

In 3D translation, we transfer the Z coordinate along with the X and Y coordinates. The process for translation in 3D is similar to 2D translation. A translation moves an object into a different position on the screen.

The following figure shows the effect of translation −

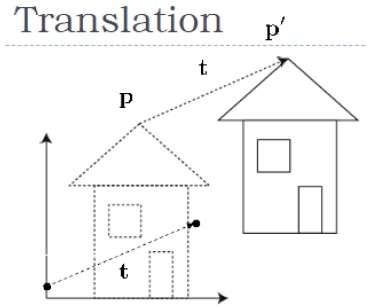
A point can be translated in 3D by adding translation coordinate $(t_{x,} t_{y,} t_{z})$ to the original coordinate (X, Y, Z) to get the new coordinate (X’, Y’, Z’).

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

P’ = P∙T

$[X′ \:\: Y′ \:\: Z′ \:\: 1] \: = \: [X \:\: Y \:\: Z \:\: 1] \: \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$

$= [X + t_{x} \:\:\: Y + t_{y} \:\:\: Z + t_{z} \:\:\: 1]$

3D Transformation

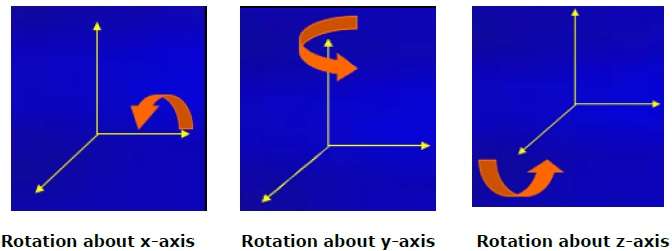
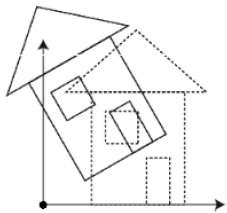
Rotation

3D rotation is not same as 2D rotation. In 3D rotation, we have to specify the angle of rotation along with the axis of rotation. We can perform 3D rotation about X, Y, and Z axes. They are represented in the matrix form as below −

$$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & −sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ −sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix} R_{z}(\theta) =\begin{bmatrix} cos\theta & −sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$$

The following figure explains the rotation about various axes −

Scaling

You can change the size of an object using scaling transformation. In the scaling process, you either expand or compress the dimensions of the object. Scaling can be achieved by multiplying the original coordinates of the object with the scaling factor to get the desired result. The following figure shows the effect of 3D scaling −

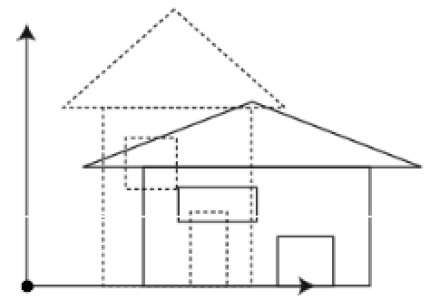
In 3D scaling operation, three coordinates are used. Let us assume that the original coordinates are (X, Y, Z), scaling factors are $(S_{X,} S_{Y,} S_{z})$ respectively, and the produced coordinates are (X’, Y’, Z’). This can be mathematically represented as shown below −

$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

P’ = P∙S

$[{X}' \:\:\: {Y}' \:\:\: {Z}' \:\:\: 1] = [X \:\:\:Y \:\:\: Z \:\:\: 1] \:\: \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$

$ = [X.S_{x} \:\:\: Y.S_{y} \:\:\: Z.S_{z} \:\:\: 1]$

Shear

A transformation that slants the shape of an object is called the shear transformation. Like in 2D shear, we can shear an object along the X-axis, Y-axis, or Z-axis in 3D.

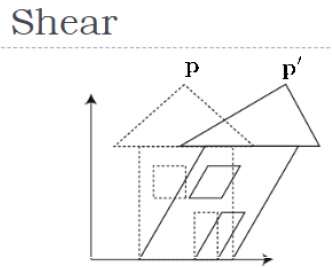
As shown in the above figure, there is a coordinate P. You can shear it to get a new coordinate P', which can be represented in 3D matrix form as below −

$Sh = \begin{bmatrix} 1 & sh_{x}^{y} & sh_{x}^{z} & 0 \\ sh_{y}^{x} & 1 & sh_{y}^{z} & 0 \\ sh_{z}^{x} & sh_{z}^{y} & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix}$

P’ = P ∙ Sh

$X’ = X + Sh_{x}^{y} Y + Sh_{x}^{z} Z$

$Y' = Sh_{y}^{x}X + Y +sh_{y}^{z}Z$

$Z' = Sh_{z}^{x}X + Sh_{z}^{y}Y + Z$

Transformation Matrices

Transformation matrix is a basic tool for transformation. A matrix with n x m dimensions is multiplied with the coordinate of objects. Usually 3 x 3 or 4 x 4 matrices are used for transformation. For example, consider the following matrix for various operation.

$T = \begin{bmatrix} 1& 0& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& 0\\ t_{x}& t_{y}& t_{z}& 1\\ \end{bmatrix}$	$S = \begin{bmatrix} S_{x}& 0& 0& 0\\ 0& S_{y}& 0& 0\\ 0& 0& S_{z}& 0\\ 0& 0& 0& 1 \end{bmatrix}$	$Sh = \begin{bmatrix} 1& sh_{x}^{y}& sh_{x}^{z}& 0\\ sh_{y}^{x}& 1 & sh_{y}^{z}& 0\\ sh_{z}^{x}& sh_{z}^{y}& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Translation Matrix	Scaling Matrix	Shear Matrix
$R_{x}(\theta) = \begin{bmatrix} 1& 0& 0& 0\\ 0& cos\theta & -sin\theta& 0\\ 0& sin\theta & cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{y}(\theta) = \begin{bmatrix} cos\theta& 0& sin\theta& 0\\ 0& 1& 0& 0\\ -sin\theta& 0& cos\theta& 0\\ 0& 0& 0& 1\\ \end{bmatrix}$	$R_{z}(\theta) = \begin{bmatrix} cos\theta & -sin\theta & 0& 0\\ sin\theta & cos\theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1 \end{bmatrix}$
Rotation Matrix

Computer Graphics Curves

In computer graphics, we often need to draw different types of objects onto the screen. Objects are not flat all the time and we need to draw curves many times to draw an object.

Types of Curves

A curve is an infinitely large set of points. Each point has two neighbors except endpoints. Curves can be broadly classified into three categories − explicit, implicit, and parametric curves.

Implicit Curves

Implicit curve representations define the set of points on a curve by employing a procedure that can test to see if a point in on the curve. Usually, an implicit curve is defined by an implicit function of the form −

f(x, y) = 0

It can represent multivalued curves (multiple y values for an x value). A common example is the circle, whose implicit representation is

x² + y² - R² = 0

Explicit Curves

A mathematical function y = f(x) can be plotted as a curve. Such a function is the explicit representation of the curve. The explicit representation is not general, since it cannot represent vertical lines and is also single-valued. For each value of x, only a single value of y is normally computed by the function.

Parametric Curves

Curves having parametric form are called parametric curves. The explicit and implicit curve representations can be used only when the function is known. In practice the parametric curves are used. A two-dimensional parametric curve has the following form −

P(t) = f(t), g(t) or P(t) = x(t), y(t)

The functions f and g become the (x, y) coordinates of any point on the curve, and the points are obtained when the parameter t is varied over a certain interval [a, b], normally [0, 1].

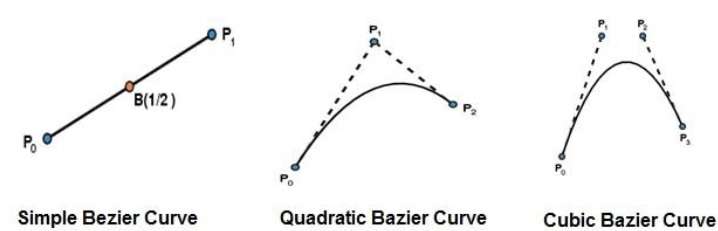
Bezier Curves

Bezier curve is discovered by the French engineer Pierre Bézier. These curves can be generated under the control of other points. Approximate tangents by using control points are used to generate curve. The Bezier curve can be represented mathematically as −

$$\sum_{k=0}^{n} P_{i}{B_{i}^{n}}(t)$$

Where $p_{i}$ is the set of points and ${B_{i}^{n}}(t)$ represents the Bernstein polynomials which are given by −

$${B_{i}^{n}}(t) = \binom{n}{i} (1 - t)^{n-i}t^{i}$$

Where n is the polynomial degree, i is the index, and t is the variable.

The simplest Bézier curve is the straight line from the point $P_{0}$ to $P_{1}$. A quadratic Bezier curve is determined by three control points. A cubic Bezier curve is determined by four control points.

Properties of Bezier Curves

Bezier curves have the following properties −

They generally follow the shape of the control polygon, which consists of the segments joining the control points.
They always pass through the first and last control points.
They are contained in the convex hull of their defining control points.
The degree of the polynomial defining the curve segment is one less that the number of defining polygon point. Therefore, for 4 control points, the degree of the polynomial is 3, i.e. cubic polynomial.
A Bezier curve generally follows the shape of the defining polygon.
The direction of the tangent vector at the end points is same as that of the vector determined by first and last segments.
The convex hull property for a Bezier curve ensures that the polynomial smoothly follows the control points.
No straight line intersects a Bezier curve more times than it intersects its control polygon.
They are invariant under an affine transformation.
Bezier curves exhibit global control means moving a control point alters the shape of the whole curve.
A given Bezier curve can be subdivided at a point t=t0 into two Bezier segments which join together at the point corresponding to the parameter value t=t0.

B-Spline Curves

The Bezier-curve produced by the Bernstein basis function has limited flexibility.

First, the number of specified polygon vertices fixes the order of the resulting polynomial which defines the curve.
The second limiting characteristic is that the value of the blending function is nonzero for all parameter values over the entire curve.

The B-spline basis contains the Bernstein basis as the special case. The B-spline basis is non-global.

A B-spline curve is defined as a linear combination of control points Pi and B-spline basis function $N_{i,}$ k (t) given by

$C(t) = \sum_{i=0}^{n}P_{i}N_{i,k}(t),$ $n\geq k-1,$ $t\: \epsilon \: [ tk-1,tn+1 ]$

Where,

{$p_{i}$: i=0, 1, 2….n} are the control points
k is the order of the polynomial segments of the B-spline curve. Order k means that the curve is made up of piecewise polynomial segments of degree k - 1,
the $N_{i,k}(t)$ are the “normalized B-spline blending functions”. They are described by the order k and by a non-decreasing sequence of real numbers normally called the “knot sequence”.

$${t_{i}:i = 0, ... n + K}$$

The N_i, k functions are described as follows −

$$N_{i,1}(t) = \left\{\begin{matrix} 1,& if \:u \: \epsilon \: [t_{i,}t_{i+1}) \\ 0,& Otherwise \end{matrix}\right.$$

and if k > 1,

$$N_{i,k}(t) = \frac{t-t_{i}}{t_{i+k-1}} N_{i,k-1}(t) + \frac{t_{i+k}-t}{t_{i+k} - t_{i+1}} N_{i+1,k-1}(t)$$

and

$$t \: \epsilon \: [t_{k-1},t_{n+1})$$

Properties of B-spline Curve

B-spline curves have the following properties −

The sum of the B-spline basis functions for any parameter value is 1.
Each basis function is positive or zero for all parameter values.
Each basis function has precisely one maximum value, except for k=1.
The maximum order of the curve is equal to the number of vertices of defining polygon.
The degree of B-spline polynomial is independent on the number of vertices of defining polygon.
B-spline allows the local control over the curve surface because each vertex affects the shape of a curve only over a range of parameter values where its associated basis function is nonzero.
The curve exhibits the variation diminishing property.
The curve generally follows the shape of defining polygon.
Any affine transformation can be applied to the curve by applying it to the vertices of defining polygon.
The curve line within the convex hull of its defining polygon.

Computer Graphics Surfaces

Polygon Surfaces

Objects are represented as a collection of surfaces. 3D object representation is divided into two categories.

Boundary Representations (B-reps) − It describes a 3D object as a set of surfaces that separates the object interior from the environment.
Space–partitioning representations − It is used to describe interior properties, by partitioning the spatial region containing an object into a set of small, non-overlapping, contiguous solids (usually cubes).

The most commonly used boundary representation for a 3D graphics object is a set of surface polygons that enclose the object interior. Many graphics system use this method. Set of polygons are stored for object description. This simplifies and speeds up the surface rendering and display of object since all surfaces can be described with linear equations.

The polygon surfaces are common in design and solid-modeling applications, since their wireframe display can be done quickly to give general indication of surface structure. Then realistic scenes are produced by interpolating shading patterns across polygon surface to illuminate.

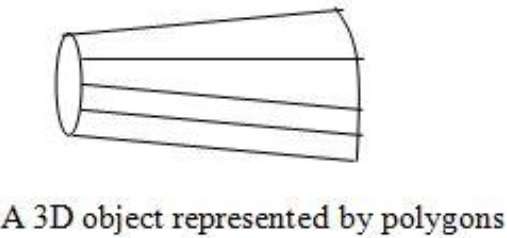
Polygon Tables

In this method, the surface is specified by the set of vertex coordinates and associated attributes. As shown in the following figure, there are five vertices, from v₁ to v₅.

Each vertex stores x, y, and z coordinate information which is represented in the table as v₁: x₁, y₁, z₁.
The Edge table is used to store the edge information of polygon. In the following figure, edge E₁ lies between vertex v₁ and v₂ which is represented in the table as E₁: v₁, v₂.
Polygon surface table stores the number of surfaces present in the polygon. From the following figure, surface S₁ is covered by edges E₁, E₂ and E₃ which can be represented in the polygon surface table as S₁: E₁, E₂, and E₃.

Plane Equations

The equation for plane surface can be expressed as −

Ax + By + Cz + D = 0

Where (x, y, z) is any point on the plane, and the coefficients A, B, C, and D are constants describing the spatial properties of the plane. We can obtain the values of A, B, C, and D by solving a set of three plane equations using the coordinate values for three non collinear points in the plane. Let us assume that three vertices of the plane are (x₁, y₁, z₁), (x₂, y₂, z₂) and (x₃, y₃, z₃).

Let us solve the following simultaneous equations for ratios A/D, B/D, and C/D. You get the values of A, B, C, and D.

(A/D) x₁ + (B/D) y₁ + (C/D) z₁ = -1

(A/D) x₂ + (B/D) y₂ + (C/D) z₂ = -1

(A/D) x₃ + (B/D) y₃ + (C/D) z₃ = -1

To obtain the above equations in determinant form, apply Cramer’s rule to the above equations.

$A = \begin{bmatrix} 1& y_{1}& z_{1}\\ 1& y_{2}& z_{2}\\ 1& y_{3}& z_{3} \end{bmatrix} B = \begin{bmatrix} x_{1}& 1& z_{1}\\ x_{2}& 1& z_{2}\\ x_{3}& 1& z_{3} \end{bmatrix} C = \begin{bmatrix} x_{1}& y_{1}& 1\\ x_{2}& y_{2}& 1\\ x_{3}& y_{3}& 1 \end{bmatrix} D = - \begin{bmatrix} x_{1}& y_{1}& z_{1}\\ x_{2}& y_{2}& z_{2}\\ x_{3}& y_{3}& z_{3} \end{bmatrix}$

For any point (x, y, z) with parameters A, B, C, and D, we can say that −

Ax + By + Cz + D ≠ 0 means the point is not on the plane.
Ax + By + Cz + D < 0 means the point is inside the surface.
Ax + By + Cz + D > 0 means the point is outside the surface.

Polygon Meshes

3D surfaces and solids can be approximated by a set of polygonal and line elements. Such surfaces are called polygonal meshes. In polygon mesh, each edge is shared by at most two polygons. The set of polygons or faces, together form the “skin” of the object.

This method can be used to represent a broad class of solids/surfaces in graphics. A polygonal mesh can be rendered using hidden surface removal algorithms. The polygon mesh can be represented by three ways −

Explicit representation
Pointers to a vertex list
Pointers to an edge list

Advantages

It can be used to model almost any object.
They are easy to represent as a collection of vertices.
They are easy to transform.
They are easy to draw on computer screen.

Disadvantages

Curved surfaces can only be approximately described.
It is difficult to simulate some type of objects like hair or liquid.

Visible Surface Detection

When we view a picture containing non-transparent objects and surfaces, then we cannot see those objects from view which are behind from objects closer to eye. We must remove these hidden surfaces to get a realistic screen image. The identification and removal of these surfaces is called Hidden-surface problem.

There are two approaches for removing hidden surface problems − Object-Space method and Image-space method. The Object-space method is implemented in physical coordinate system and image-space method is implemented in screen coordinate system.

When we want to display a 3D object on a 2D screen, we need to identify those parts of a screen that are visible from a chosen viewing position.

Depth Buffer (Z-Buffer) Method

This method is developed by Cutmull. It is an image-space approach. The basic idea is to test the Z-depth of each surface to determine the closest (visible) surface.

In this method each surface is processed separately one pixel position at a time across the surface. The depth values for a pixel are compared and the closest (smallest z) surface determines the color to be displayed in the frame buffer.

It is applied very efficiently on surfaces of polygon. Surfaces can be processed in any order. To override the closer polygons from the far ones, two buffers named frame buffer and depth buffer, are used.

Depth buffer is used to store depth values for (x, y) position, as surfaces are processed (0 ≤ depth ≤ 1).

The frame buffer is used to store the intensity value of color value at each position (x, y).

The z-coordinates are usually normalized to the range [0, 1]. The 0 value for z-coordinate indicates back clipping pane and 1 value for z-coordinates indicates front clipping pane.

Algorithm

Step-1 − Set the buffer values −

Depthbuffer (x, y) = 0

Framebuffer (x, y) = background color

Step-2 − Process each polygon (One at a time)

For each projected (x, y) pixel position of a polygon, calculate depth z.

If Z > depthbuffer (x, y)

Compute surface color,

set depthbuffer (x, y) = z,

framebuffer (x, y) = surfacecolor (x, y)

Advantages

It is easy to implement.
It reduces the speed problem if implemented in hardware.
It processes one object at a time.

Disadvantages

It requires large memory.
It is time consuming process.

Scan-Line Method

It is an image-space method to identify visible surface. This method has a depth information for only single scan-line. In order to require one scan-line of depth values, we must group and process all polygons intersecting a given scan-line at the same time before processing the next scan-line. Two important tables, edge table and polygon table, are maintained for this.

The Edge Table − It contains coordinate endpoints of each line in the scene, the inverse slope of each line, and pointers into the polygon table to connect edges to surfaces.

The Polygon Table − It contains the plane coefficients, surface material properties, other surface data, and may be pointers to the edge table.

To facilitate the search for surfaces crossing a given scan-line, an active list of edges is formed. The active list stores only those edges that cross the scan-line in order of increasing x. Also a flag is set for each surface to indicate whether a position along a scan-line is either inside or outside the surface.

Pixel positions across each scan-line are processed from left to right. At the left intersection with a surface, the surface flag is turned on and at the right, the flag is turned off. You only need to perform depth calculations when multiple surfaces have their flags turned on at a certain scan-line position.

Area-Subdivision Method

The area-subdivision method takes advantage by locating those view areas that represent part of a single surface. Divide the total viewing area into smaller and smaller rectangles until each small area is the projection of part of a single visible surface or no surface at all.

Continue this process until the subdivisions are easily analyzed as belonging to a single surface or until they are reduced to the size of a single pixel. An easy way to do this is to successively divide the area into four equal parts at each step. There are four possible relationships that a surface can have with a specified area boundary.

Surrounding surface − One that completely encloses the area.
Overlapping surface − One that is partly inside and partly outside the area.
Inside surface − One that is completely inside the area.
Outside surface − One that is completely outside the area.

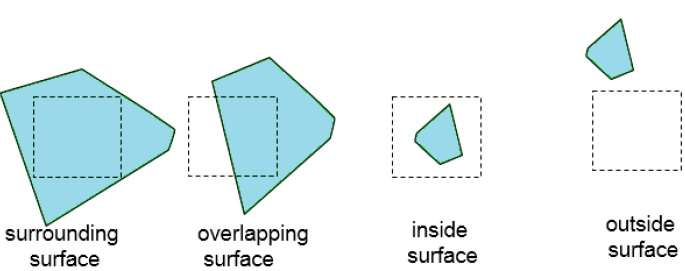
The tests for determining surface visibility within an area can be stated in terms of these four classifications. No further subdivisions of a specified area are needed if one of the following conditions is true −

All surfaces are outside surfaces with respect to the area.
Only one inside, overlapping or surrounding surface is in the area.
A surrounding surface obscures all other surfaces within the area boundaries.

Back-Face Detection

A fast and simple object-space method for identifying the back faces of a polyhedron is based on the "inside-outside" tests. A point (x, y, z) is "inside" a polygon surface with plane parameters A, B, C, and D if When an inside point is along the line of sight to the surface, the polygon must be a back face (we are inside that face and cannot see the front of it from our viewing position).

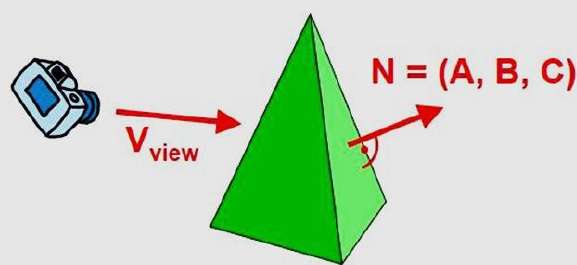
We can simplify this test by considering the normal vector N to a polygon surface, which has Cartesian components (A, B, C).

In general, if V is a vector in the viewing direction from the eye (or "camera") position, then this polygon is a back face if

V.N > 0

Furthermore, if object descriptions are converted to projection coordinates and your viewing direction is parallel to the viewing z-axis, then −

V = (0, 0, V_z) and V.N = V_ZC

So that we only need to consider the sign of C the component of the normal vector N.

In a right-handed viewing system with viewing direction along the negative $Z_{V}$ axis, the polygon is a back face if C < 0. Also, we cannot see any face whose normal has z component C = 0, since your viewing direction is towards that polygon. Thus, in general, we can label any polygon as a back face if its normal vector has a z component value −

C <= 0

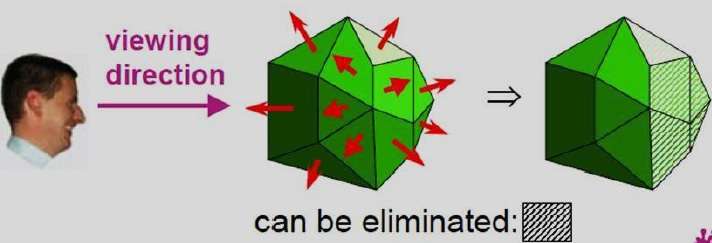
Similar methods can be used in packages that employ a left-handed viewing system. In these packages, plane parameters A, B, C and D can be calculated from polygon vertex coordinates specified in a clockwise direction (unlike the counterclockwise direction used in a right-handed system).

Also, back faces have normal vectors that point away from the viewing position and are identified by C >= 0 when the viewing direction is along the positive $Z_{v}$ axis. By examining parameter C for the different planes defining an object, we can immediately identify all the back faces.

A-Buffer Method

The A-buffer method is an extension of the depth-buffer method. The A-buffer method is a visibility detection method developed at Lucas film Studios for the rendering system Renders Everything You Ever Saw (REYES).

The A-buffer expands on the depth buffer method to allow transparencies. The key data structure in the A-buffer is the accumulation buffer.

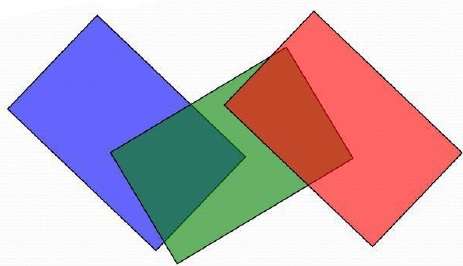
Each position in the A-buffer has two fields −

Depth field − It stores a positive or negative real number
Intensity field − It stores surface-intensity information or a pointer value

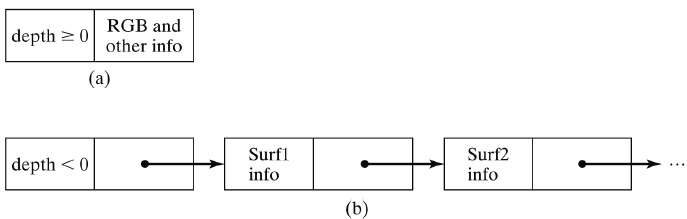
If depth >= 0, the number stored at that position is the depth of a single surface overlapping the corresponding pixel area. The intensity field then stores the RGB components of the surface color at that point and the percent of pixel coverage.

If depth < 0, it indicates multiple-surface contributions to the pixel intensity. The intensity field then stores a pointer to a linked list of surface data. The surface buffer in the A-buffer includes −

RGB intensity components
Opacity Parameter
Depth
Percent of area coverage
Surface identifier

The algorithm proceeds just like the depth buffer algorithm. The depth and opacity values are used to determine the final color of a pixel.

Depth Sorting Method

Depth sorting method uses both image space and object-space operations. The depth-sorting method performs two basic functions −

First, the surfaces are sorted in order of decreasing depth.
Second, the surfaces are scan-converted in order, starting with the surface of greatest depth.

The scan conversion of the polygon surfaces is performed in image space. This method for solving the hidden-surface problem is often referred to as the painter's algorithm. The following figure shows the effect of depth sorting −

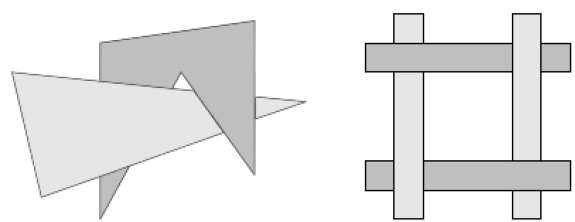
The algorithm begins by sorting by depth. For example, the initial “depth” estimate of a polygon may be taken to be the closest z value of any vertex of the polygon.

Let us take the polygon P at the end of the list. Consider all polygons Q whose z-extents overlap P’s. Before drawing P, we make the following tests. If any of the following tests is positive, then we can assume P can be drawn before Q.

Do the x-extents not overlap?
Do the y-extents not overlap?
Is P entirely on the opposite side of Q’s plane from the viewpoint?
Is Q entirely on the same side of P’s plane as the viewpoint?
Do the projections of the polygons not overlap?

If all the tests fail, then we split either P or Q using the plane of the other. The new cut polygons are inserting into the depth order and the process continues. Theoretically, this partitioning could generate O(n²) individual polygons, but in practice, the number of polygons is much smaller.

Binary Space Partition (BSP) Trees

Binary space partitioning is used to calculate visibility. To build the BSP trees, one should start with polygons and label all the edges. Dealing with only one edge at a time, extend each edge so that it splits the plane in two. Place the first edge in the tree as root. Add subsequent edges based on whether they are inside or outside. Edges that span the extension of an edge that is already in the tree are split into two and both are added to the tree.

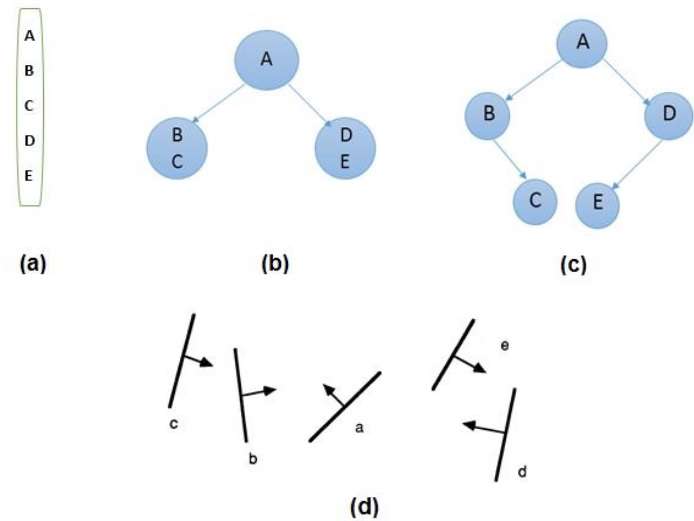
From the above figure, first take A as a root.
Make a list of all nodes in figure (a).
Put all the nodes that are in front of root A to the left side of node A and put all those nodes that are behind the root A to the right side as shown in figure (b).
Process all the front nodes first and then the nodes at the back.
As shown in figure (c), we will first process the node B. As there is nothing in front of the node B, we have put NIL. However, we have node C at back of node B, so node C will go to the right side of node B.
Repeat the same process for the node D.

Computer Graphics Fractals

A French/American mathematician Dr Benoit Mandelbrot discovered Fractals. The word fractal was derived from a Latin word fractus which means broken.

What are Fractals?

Fractals are very complex pictures generated by a computer from a single formula. They are created using iterations. This means one formula is repeated with slightly different values over and over again, taking into account the results from the previous iteration.

Fractals are used in many areas such as −

Astronomy − For analyzing galaxies, rings of Saturn, etc.
Biology/Chemistry − For depicting bacteria cultures, Chemical reactions, human anatomy, molecules, plants,
Others − For depicting clouds, coastline and borderlines, data compression, diffusion, economy, fractal art, fractal music, landscapes, special effect, etc.

Generation of Fractals

Fractals can be generated by repeating the same shape over and over again as shown in the following figure. In figure (a) shows an equilateral triangle. In figure (b), we can see that the triangle is repeated to create a star-like shape. In figure (c), we can see that the star shape in figure (b) is repeated again and again to create a new shape.

We can do unlimited number of iteration to create a desired shape. In programming terms, recursion is used to create such shapes.

Geometric Fractals

Geometric fractals deal with shapes found in nature that have non-integer or fractal dimensions. To geometrically construct a deterministic (nonrandom) self-similar fractal, we start with a given geometric shape, called the initiator. Subparts of the initiator are then replaced with a pattern, called the generator.

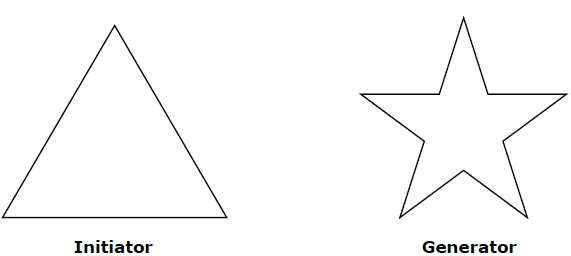
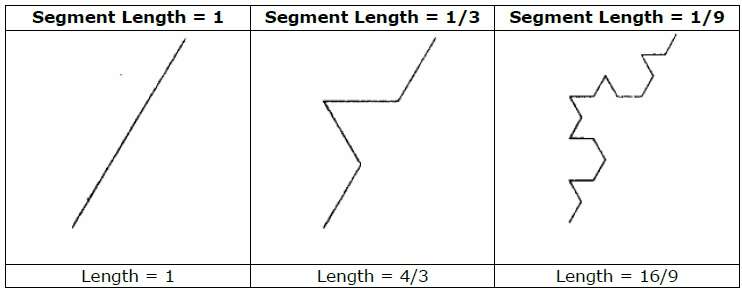
As an example, if we use the initiator and generator shown in the above figure, we can construct good pattern by repeating it. Each straight-line segment in the initiator is replaced with four equal-length line segments at each step. The scaling factor is 1/3, so the fractal dimension is D = ln 4/ln 3 ≈ 1.2619.

Also, the length of each line segment in the initiator increases by a factor of 4/3 at each step, so that the length of the fractal curve tends to infinity as more detail is added to the curve as shown in the following figure −

Computer Animation

Animation means giving life to any object in computer graphics. It has the power of injecting energy and emotions into the most seemingly inanimate objects. Computer-assisted animation and computer-generated animation are two categories of computer animation. It can be presented via film or video.

The basic idea behind animation is to play back the recorded images at the rates fast enough to fool the human eye into interpreting them as continuous motion. Animation can make a series of dead images come alive. Animation can be used in many areas like entertainment, computer aided-design, scientific visualization, training, education, e-commerce, and computer art.

Animation Techniques

Animators have invented and used a variety of different animation techniques. Basically there are six animation technique which we would discuss one by one in this section.

Traditional Animation (frame by frame)

Traditionally most of the animation was done by hand. All the frames in an animation had to be drawn by hand. Since each second of animation requires 24 frames (film), the amount of efforts required to create even the shortest of movies can be tremendous.

Keyframing

In this technique, a storyboard is laid out and then the artists draw the major frames of the animation. Major frames are the ones in which prominent changes take place. They are the key points of animation. Keyframing requires that the animator specifies critical or key positions for the objects. The computer then automatically fills in the missing frames by smoothly interpolating between those positions.

Procedural

In a procedural animation, the objects are animated by a procedure − a set of rules − not by keyframing. The animator specifies rules and initial conditions and runs simulation. Rules are often based on physical rules of the real world expressed by mathematical equations.

Behavioral

In behavioral animation, an autonomous character determines its own actions, at least to a certain extent. This gives the character some ability to improvise, and frees the animator from the need to specify each detail of every character's motion.

Performance Based (Motion Capture)

Another technique is Motion Capture, in which magnetic or vision-based sensors record the actions of a human or animal object in three dimensions. A computer then uses these data to animate the object.

This technology has enabled a number of famous athletes to supply the actions for characters in sports video games. Motion capture is pretty popular with the animators mainly because some of the commonplace human actions can be captured with relative ease. However, there can be serious discrepancies between the shapes or dimensions of the subject and the graphical character and this may lead to problems of exact execution.

Physically Based (Dynamics)

Unlike key framing and motion picture, simulation uses the laws of physics to generate motion of pictures and other objects. Simulations can be easily used to produce slightly different sequences while maintaining physical realism. Secondly, real-time simulations allow a higher degree of interactivity where the real person can maneuver the actions of the simulated character.

In contrast the applications based on key-framing and motion select and modify motions form a pre-computed library of motions. One drawback that simulation suffers from is the expertise and time required to handcraft the appropriate controls systems.

Key Framing

A keyframe is a frame where we define changes in animation. Every frame is a keyframe when we create frame by frame animation. When someone creates a 3D animation on a computer, they usually don’t specify the exact position of any given object on every single frame. They create keyframes.

Keyframes are important frames during which an object changes its size, direction, shape or other properties. The computer then figures out all the in-between frames and saves an extreme amount of time for the animator. The following illustrations depict the frames drawn by user and the frames generated by computer.

Morphing

The transformation of object shapes from one form to another form is called morphing. It is one of the most complicated transformations.

A morph looks as if two images melt into each other with a very fluid motion. In technical terms, two images are distorted and a fade occurs between them.